Dynamika rotorových soustav
9. Vyvažování rotorů
Obsah
1. Úvod
2. Hmotné momenty setrvačnosti
3. Vyvažování tuhých rotorů
4. Dynamické vlastnosti rotorových soustav
5. Vyvažování pružných rotorů
1. Úvod
S ohledem na to, že vyvažování tuhých rotorů vychází z analýzy rotačního pohybu, bude nejdříve proveden výklad momentů setrvačnosti. Poté bude následovat analýza rotačního pohybu. Následovat bude teoretický základ dynamických vlastností rotorových soustav a zakončení bude provedeno analýzou vyvažování pružných rotorů.
Na začátek je nutno vymezit pojem tuhého a pružného rotoru. K tomu existuje několik definic, všechny jsou však založeny na vzájemné relaci dynamických vlastností a maximálních provozních otáčkách.
Definice tuhého a pružného rotoru
Jestliže je celková potenciální energie akumulovaná v ložiskách větší než 80% celkové potenciální energie, rotor je klasifikován jako tuhý. Celková potenciální energie se skládá z energie napjatosti a klasické potenciální energie.
Hmotné momenty setrvačnosti
Při analýze dynamických vlastností tuhého tělesa se vyskytují závislosti rozložení hmotnosti na jeho geometrických souřadnicích. Tyto hmotné momenty setrvačnosti se označují jako druhé momenty. První momenty se označují jako statické a slouží zejména pro určení polohy těžiště.
Statické momenty
Hmotné momenty setrvačnosti
a. Rovinný
b. Osový
c. Polární
d. Deviační
a. Rovinný
k rovině 
k rovině 
k rovině 
b. Osový
k ose 
k ose 
k ose 
c. Polární
k bodu 
d. Deviační
k osám 
k osám 
k osám 
Dále platí
Poloměr setrvačnosti
Tenzor setrvačnosti
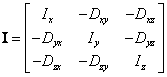
Momenty setrvačnosti k posunutým osám
Steinerova věta
P – značí počátek posunutého souřadnicového systému
T – značí těžiště tělesa
Momenty setrvačnosti k natočeným osám
Transformační matice
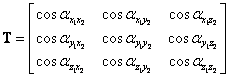
kde horní index T značí transpozici
Hlavní osa setrvačnosti
Hlavní setrvačný systém je takový, ke kterému jsou deviační momenty nulové
Poznámky:
· Má-li těleso osu symetrie, pak tato osa je hlavní centrální osou setrvačnosti a každé dvě přímky k ní kolmé jsou hlavními osami setrvačnosti pro bod na ose symetrie
· Má-li těleso rovinu symetrie, pak každá přímka k ní kolmá je hlavní osou setrvačnosti pro bod v průsečíku osy s rovinou
· Má-li těleso dvě roviny symetrie, pak průsečnice těchto rovin je hlavní centrální osou setrvačnosti
Stanovení momentů setrvačnosti
· Výpočet (viz tabulky)
· Experimentálně - odkýváním
Experimentální stanovení momentů setrvačnosti
Bifilární kyvadlo – těleso zavěšené na dvou stejně dlouhých, rovnoběžných a nehmotných vláknech.
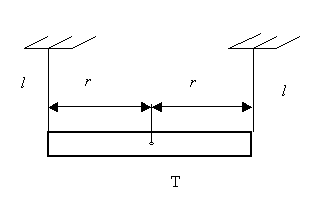
kde 
– hmotnost 
– gravitační zrychlení 
– vzdálenost těžiště od
závěsu 
- doba kyvu 
2. Analýza rotačního pohybu tělesa
Na obrázku je nakreslen pohled na těleso, které koná rotační pohyb ve směru osy rotace. Poloha těžiště je dána souřadnicí x.
Význam veličin:
T - těžiště
-
poloha elementu dm
-
úhlová rychlost
- úhlové zrychlení
- výslednice sil ve směru
osy x, včetně vnějšího zatížení a sil v ložiskách
- výslednice sil ve směru
osy y, včetně vnějšího zatížení a sil v ložiskách
- výslednice sil ve směru
osy z, včetně vnějšího zatížení a sil v ložiskách
- výsledný moment k ose x
- výsledný moment k ose y,
který zahrnuje i momenty od sil v ložiskách
- výsledný moment k ose z,
který zahrnuje i momenty od sil v ložiskách
- poloha těžiště ve směru
osy x od počátku
Pro zrychlení elementu dm platí
Pro těžiště platí
Pohybové rovnice pro síly
Pohybové rovnice pro momenty
Po dosazení za zrychlení
Pohybové rovnice pro momenty
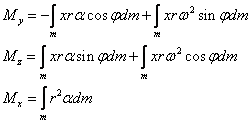
Úhlové zrychlení i úhlová rychlost jsou kinematické veličiny tělesa a nejsou závislé na poloze hmotného elementu dm. Proto je lze vytknout před integrál.
Po úpravě pak je
Pohybové rovnice pro momenty
V rovnicích pro síly lze
integrály nahradit statickými momenty, ve kterých se bude vyskytovat těžiště a
v momentových rovnicích a představují integrály deviační
momenty a v momentové rovnici představuje integrál osový moment
setrvačnosti k ose x, tedy k ose rotace.
Po úpravě je
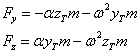
Pohybové rovnice pro momenty
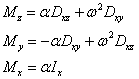
Závěr
V pohybových rovnicích pro síly je zatížení ložisek, které je zahrnuto v silách na levé straně rovnice, závislé na úhlové rychlosti a zrychlení otáčení rotoru i na poloze těžiště. Při nenulových otáčkách je nutno pro eliminaci zatížení dosáhnout toho, aby těžiště leželo na ose rotace. To je cílem statického vyvažování. V tomto případě se eliminuje silový účinek. Vzhledem k tomu, že silová výslednice má charakter volného vektoru, tzn. nezávisí na poloze, může být vyvažovací rovina ve kterémkoliv místě po délce rotoru. Rovněž je zřejmé, že vzhledem k tomu, že se eliminuje silový účinek, stačí rovina jedna. Rovněž je zřejmé, že z pohledu statické ekvivalence lze silový účinek jedné síly nahradit silovým účinkem více sil, pak lze staticky vyvažovat i ve více rovinách. Statické vyvažování, jak bude dále ukázáno, lze provádět i za klidu.
Stále však ještě je
silové zatížení ložisek (reakce) v momentových rovnicích. V tomto
případě je nutno pro nenulové otáčky dosáhnou toho, aby deviační momenty 
a 
byly nulové. To
je cílem dynamického vyvažování. V obou deviačních momentech se
vyskytuje osa rotace x. To znamená, že pro nulové deviační momenty musí
být tato osa rovněž hlavní osou setrvačnosti. Cílem dynamického vyvažování tedy
je dosáhnout toho, aby osa rotace byla hlavní osou setrvačnosti. Vzhledem
k tomu, že se účinek nevývahy tohoto druhu vyskytuje v momentových
rovnicích, jsou nutné roviny dvě. Z pohledu statiky představuje totiž
moment dvojici sil, což jsou dvě stejně velké síly na rovnoběžných nositelkách
a opačně orientované. Dvě nositelky tak představují minimálně dvě vyvažovací
roviny. Stejně jako v případě ekvivalence u sil, platí i ekvivalence u
momentů, pak lze dynamicky vyvažovat i ve více rovinách. Dynamické vyvažování
se musí provádět za rotace. Jestliže se předpokládá, že rotor je staticky
vyvážen, tento druh nevývahy se projeví pouze za rotace.
Shrneme-li statické i dynamické vyvažování, které představuje snížení dynamického zatížení v ložiskách na minimální hodnotu, cílem obou vyvažování je dosáhnout toho, aby osa rotace byla hlavní centrální osou setrvačnosti.
Metody statického vyvažování
· za klidu
· za rotace
Za klidu
a) Metoda zkusmo
Vyvažuje se na vyvažovacích trnech. Rotor je umístěn na trnech, a tak dlouho se přidává, nebo ubírá hmotnost, až rotor zůstane při jakémkoliv pootočení v klidové poloze. Tímto způsobem se provádí pouze statické vyvažování. Cílem je eliminace tíhového účinku.
b) Pomocí jednotkové hmoty (koeficientu vlivu)
Rotor se
v prvním kroku nechá ustálit, čímž se zjistí poloha těžiště. Ve druhém
kroku se přidá pod známým úhlem 
(zpravidla 
) známá nevývaha 
a opět se nechá
rotor ustálit.
Pro vyvážený rotor musí platit
Také je
Odkud
Pak
Za rotace
Princip statického vyvažování za rotace je obdobný. V tomto případě je větší účinek odstředivé síly. Zpravidla bývá tříkrokové.
1.
krok - Zjistí se vektor kmitání 
nevyváženého rotoru.
2.
krok - Ve zvoleném místě se přidá známá nevývaha 
a změří se vektor kmitání
.
3.
krok – Zjistí se účinek nevývahy, který je dán vektorem 
. Odměří se úhel
.
Velikost nevývahy, která se přidá je
Orientace, kterým se nanáší od
výchozí polohy 
je dána smyslem úhlu , který je
v tomto případě orientovaný.
Dynamické vyvažování je obdobou statického za rotace, pouze je třeba si uvědomit, že moment je účinek dvojice sil.
3. Dynamické vlastnosti rotorových soustav
Úlohy
1. Frekvenčně modální vlastnosti
2. Odezva při vynuceném ustáleném kmitání
3. Odezva při přechodovém kmitání
4. Problém stability
Metody
1. Metoda konečných prvků - MKP
2. Metoda dynamických poddajností – MDP, modální metoda MM
3. Modální transformace
Úvod
Gyroskopické účinky
Résalovo úhlové zrychlení
Gyroskopický moment (setrvačný účinek)
Campbellův diagram
3.1. Frekvenčně modální vlastnosti
Aplikace MKP
Pohybová rovnice
Transformace do stavového prostoru
Substituce (jsou i jiné možnosti)
Pohybová rovnice pak má tvar
Pak lze psát
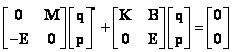
kde je - vektor stavu 
Nebo zkráceně
Řešení
Po dosazení
Stanovení: - vlastní frekvence
- vlastní tvary (pravostranné), modální matice
Levostranné vektory
Úprava – transponování celé rovnice
Po úpravě
Řešení
Po dosazení
Stanovení: - vlastní frekvence
- vlastní tvary (levostranné), modální matice
Normování
Komplexní vlastní číslo
Matice dynamických poddajností
Pohybová rovnice
Řešení
Po dosazení
Nebo také
kde 
- matice dynamických poddajností
Také je
kde 
- matice dynamických tuhostí
Pro matici dynamických poddajností také platí
kde v čitateli je tzv. dyadický součin
3.2 Odezva při vynuceném ustáleném kmitání
Předpoklad – harmonické buzení 
Pohybová rovnice
Řešení
Po dosazení
Nebo také
Výstupy:
§ Amplitudo frekvenční charakteristika
§ Fázová frekvenční charakteristika
§ Pancuovy – Kennedyho diagramy
§ Bodyho diagramy
Vyjádření: Amplituda, fáze
sin-ová a cos-inová složka
reálná a imaginární část
Řešení úloh na bázi MKP
Výchozí nelineární pohybová rovnice pro předpoklad buzení vlastní nevývahou má tvar
Pro předpoklad harmonického kmitání pro odezvu platí
5. Vyvažování pružných rotorů
Metody vyvažování (týkají se tuhých i pružných rotorů)
Poznámky
§ Koeficienty vlivu – příčinkové koeficienty
1. Vyvažování v jedné rovině s využitím koeficientů vlivu
Je to nejjednodušší metoda vyvažování. Využívá se známého vývažku, který se umístí do známého místa a zjišťuje se účinek této nevývahy. Měří se amplituda a fáze kmitání. Pomocí těchto veličin se stanoví vliv jednotkové nevývahy a vypočítá se nevývaha, která je nutná pro dovážení rotoru. Tato metoda porývá 90% všech vyvažování. V této metodě je v podstatě zjišťován jeden koeficient “vlivu” nevývahy na vibrace.
2. Vyvažování ve dvou rovinách s využitím koeficientů vlivu
Metoda je značně podobná předchozí. Nejdříve se dá známá nevývaha do jednoho místa a stanoví se dva koeficienty vlivu této nevývahy na vibrace. Poté se dá známá nevývaha do druhého místa a opět se zjistí dva koeficienty vlivu. Poté se na základě řešení soustavy dvou komplexních rovnic (4 reálných) stanoví dva nevývažky a dvě polohy, ve kterých se nevývažky umístí. Metoda je v podstatě exaktní.
3. Vyvažování ve dvou rovinách s využitím statické a dynamické složky
Je to metoda velmi podobná vyvažování v jedné rovině, v tomto případě jsou měřeny amplitudy a fáze ve dvou místech na rotoru (mohou to být konce hřídele). Podle toho, jestli převažuje účinek nevývahy jako statický, nebo dynamický, se rotor vyvažuje. Staticky v jedné rovině, která prochází osou hřídele, přičemž na základě vektorové závislosti se zjistí nevývaha a místo, kde se má umístit. Jestli převažuje dynamický účinek, vyvažuje se ve dvou rovinách a druhá nevývaha se dává 180 stupňů vzhledem k první. Tato metoda je v podstatě nejjednodušší modální metodou, která používá znalosti tzv. koeficientů vlivu.
4. Vyvažování v jedné rovině s využitím koeficientů vlivu a s využitím lineární regrese
Využívá se jedné roviny a jedněch otáček. Při těchto otáčkách je možné rotor převážit tak, aby v kritických otáčkách byl vyvážen. Metoda lineární regrese je nejjednodušší metodou nejmenších čtverců. Tato metoda se používá, pokud je rotor ohnut, nebo má počáteční házení.
5. Zobecněná metoda s využitím koeficientů vlivu a pseudoinverse
Metoda je založena na využití dvou a více vyvažovacích rovin a měření při více otáčkách. Metoda je někdy nazývána jako metoda pseudoinverse, nebo metoda nejmenších čtverců. Metoda vede k cíli i u rotorů turbogenerátorů. Metoda je výhodná mimo jiné také tím, že se nemusí znát hodně o systému celého rotou a jeho dynamického chování. Jsou známy poznatky úspěšného vyvážení i pružných rotorů, které přecházely 5 kritických otáček. Jestliže jsou nesprávně voleny roviny, vede to k velkým nevývažkům v jiných rovinách. Metoda nemůže zabezpečit neúměrné nevývahy v různých rovinách.
6. Vyvažování ve více rovinách při použití lineárního programování
Je to v podstatě předchozí metoda, ale kombinuje se zde výpočtové modelování koeficientů vlivu. V podstatě experimentální analýza je doplněna výpočtovým modelováním. Kombinují se výsledky experimentu s výsledky výpočtového modelování.
7. Modální vyvažování
Metoda je vhodná zejména pro pružné rotory, které přecházejí přes několik kritických otáček. Při této metodě musí být známy tvary kmitání při kritických otáčkách. Tyto lze stanovit ať už výpočtem, nebo také experimentálně. Základem modálního vyvažování je vyvažovat rotor s velkým faktorem zesílení u daného tvaru kmitu, aniž by se rozrušily ostatní tvary kmitu. Tzv. modální nevývahy jsou počítány na základě metody koeficientů vlivu, které jsou stanoveny experimentálně. Byla rovněž publikována metoda sjednoceného (kombinovaného) modálního a příčinkového vyvažování. Zpřesnění metody závisí na znalosti tvarů kmitání, které mohou být komplexní.
8. Metoda tří váhových zkoušek
Je známo hodně případů, ve kterých není možné získat přesné výsledky, na základě kterých se má rozhodnout kam umístit vývažky (amplitudy i fáze). Proto byla navržena metoda tří zkušebních nevývah a čtyř běhů. Při třech bězích se postupně umísťuje nevývaha ve třech rozdílných místech na rotoru. Cílem je stanovit amplitudu kmitání při nevývaze a místo pro umístění vývažku. Metoda je velmi vhodná pro nelineární rotorové soustavy. Může být použita i jako grafická, pak není nutný výpočet. Byla použita u vyvažování rotorů s ventilátory, kde proud vzduchu v kole způsoboval nestacionární vibrace rotoru, včetně kolísání otáček.
9. Metoda vyvažování ve více rovinách bez fáze
Tato metoda je rozšířením metody tří váhových zkoušek na pružné rotory. Toto rozšíření spočívá v tom, že rozmístění testovacích vývažků na rotoru odpovídá danému tvaru kmitání. Při vyvažování je nutný záznam dat a následná spektrální analýza (FFT). Tím se stanoví pro danou frekvenci (dané kritické otáčky a tedy i daný tvar kmitání) amplitudy kmitání. Každý tvar kmitu se musí vyvážit samostatně a navíc pro tři testovací nevývahy. Metoda se používá tam, kde všechny ostatní metody selhávají, zejména „metoda vyvažování ve více rovinách při použití lineárního programování“. Nevýhodou této metody je, že musí být známy tvary kmitání a pro každé kritické otáčky musí být provedeny tři samostatné běhy.
10. Metoda vyvažování bez tří běhů
Tato metoda, bez zkušební (testovací) nevývahy je nazývána také jako metoda jednoho výstřelu (jednoho zásahu). Velikost nevývahy je stanovena na základě měření vibrací a berou se v úvahu i koeficienty vlivu. Místo a velikost nevývahy je stanoveno na základě Nyquistova diagramu. Na základě toho je stanoven tzv.modální vývažek, který je stanoven při daných otáčkách, které jsou co nejblíže kritickým. Nyquistovy diagramy jsou kresleny pro oba směry kolmé na osu rotace. Nevýhodou metody je, že musí být znám tzv. „vynucený“ tvar kmitu pro otáčky, při kterých se provádí vyvažování. Tato metoda se používá jako startovací pro jiné metody.
Obecná metoda vyvažování ve dvou rovinách
Předpokládejme, že rotor je staticky vyvážen, tedy těžiště leží na ose rotace. Avšak osa rotace není hlavní osou setrvačnosti.
Vyvažování se děje ve dvou rovinách a vibrace jsou měřeny ve druhých dvou rovinách. Je dobré, když dvě roviny jsou vzdáleny od sebe co nejdále a v příslušných místech jsou místa kde se měří vibrace a kde se provádí vyvažování co nejblíže. Tedy rovina, ve které se měří vibrace a ve kterých se provádí vibrace jsou blízko sobě.
Poznámka
· Všechny veličiny jsou komplexní
Vibrace jsou měřeny ve dvou rovinách, které označme a a b. Vyvažování je měřeno také ve dvou rovinách, které v obecném případě nemusí být totožné s rovinami, ve kterých se provádí měření. Označme neznámou nevývahu n , testovací nevývaha t a neznámý vývažek který je nutno stanovit z. Pak pro měřené vibrace platí vztah
Aby bylo možné vypočítat vývažek,
je nutno znát 4 koeficienty vlivu (příčinkové koeficienty), nebo také 4
koeficienty matice dynamických poddajností 
.
Testovací, zkušební nevývaha se umístí do místa vyvažování 1. Jsou měřeny nové hodnoty vibrací.
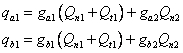
Z těchto dvou měření lze
stanovit koeficienty 
pro které platí
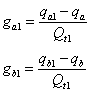
Pro stanovení zbývajících dvou koeficientů je nutno dát známou testovací nevývahu do místa b. Vztahy pro výpočet zbývajících dvou koeficientů by byly obdobné. Pokud však přidáním nevývah do místa a se vibrace zlepšily, není nutno je odsud dávat pryč, ale pouze přidat další nevývahy do místa b. Předpokládejme dále, což je obecnější případ, že testovací nevývahy v místě a necháme. Pak pro novou měřenou odezvu platí
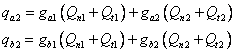
Odtud se zbývající dva koeficienty vlivu, nebo také prvky matice dynamických poddajností stanoví dle vztahu
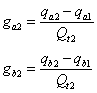
Jestliže jsou všechny testovací nevývahy oddělány, pak nevývahy, které je třeba přidat v místech vyvažovacích rovin jsou dány vztahy
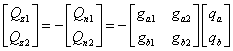
Vyvažování pružných rotorů ve více rovinách
Rotor je označován také jako pružný, jestliže po jeho vyvážení jako rotoru tuhého, vykazuje při vyšších otáčkách zvýšené vibrace.
Otázka počtu vyvažovacích rovin pružných rotorů
Předpokládejme, že je dán prizmatický rotor se dvěma tuhými ložisky. Pak pro n tvarů kmitání má rotor n+1 uzlových bodů po délce. Vyvažování v uzlech nemá vliv na vyvážení tohoto tvaru kmitu v rozsahu 20% kolem těchto kritických otáček. Odtud, počet tzv. aktivních vyvažovacích rovin pro prizmatický hřídel rotorové soustavy při vyvážení n tvarů kmitání je dán počtem rovin, kde není uzel, minus počet míst, kde je nulová výchylka, tedy
Odtud je zřejmé, že pro vyvážení prvního tvaru kmitu stačí jedna vyvažovací rovina. Vyvážení dvou tvarů kmitu vyžaduje dvě roviny. To je tzv. n-metoda vyvažování. Dlouhé a zejména rotory turbogenerátorů vyžadují více vyvažovacích rovin. Proto se vyžaduje takové rotory vyvažovat v n+2 rovinách. To je dáno tím, že v rozsahu otáček mimo rezonance (mimo kritické otáčky kmitá rotor vynuceným tvarem kmitu, na kterém se podílí i vyšší vlastní tvary kmitu)
Poznámka
· vlastní tvar kmitu
· vynucený tvar kmitu
Další vlivy na počet rovin
· tuhost ložisek
· místa vyvažování
· provozní podmínky (konstantní, nebo proměnné otáčky)
· nelineární vlastnosti – tekutinové vrstvy
· vazba s okolním prostředím
· spojení spojkou s jinými částmi
· bezpečnostní spolehlivost (jaderná energetika)
Modální vyvažování pružných rotorů
Zobecněná pohybová rovnice rotoru, při buzení nevývahou a zahrnující gyroskopické účinky a tlumení při dané nevývaze má tvar
kde 
- je neznámá nevývaha na rotoru,
kterou je nutno eliminovat dovážením
Předpokládejme odezvu rovněž ve tvaru
Pro odezvu na rotoru lze také napsat
nebo také
Jednotlivé sčítance jsou
kde 
je pro daný
tvar kmitu skalární veličina
V případě, že se vyvažuje
blízko vlastní frekvence, (v blízkosti daných kritických otáček), tedy 
, pak pro daný
tvar kmitu je
Tlumení 
pro i-tý
tvar kmitu lze zahrnout do vlastního tvaru kmitu. Pak
lze tuto rovnici po formální stránce přepsat do tvaru
Předpokládejme, že budeme vyvažovat p tvarů kmitání v p rovinách. Pro odezvu na rotoru pak platí
kde jednotlivé členy nabývají hodnot
Poznámky
· pro netlumenou soustavu je v rezonanci teoreticky nekonečně velká odezva
· příspěvek vyšších tvarů kmitání je zanedbatelný
· v p tvarech mohou být zahrnuty i vyšší, např. ve smyslu počtu rovin o dvě vyšší
Vztah pro odezvu pak lze zapsat ve tvaru
kde 
je reziduální odezva od vyšších
tvarů kmitu, které nejsou vyvažovány a jejich příspěvek k celkové odezvě je
zanedbatelný.
Vyvažováním se chce dosáhnout
toho, aby při doplnění vývažku 
byla výchylka 
. Toho lze dosáhnout tím,
že se přidá k dané rotorové soustavě vývažek, přičemž při jeho přidání
bude odezva na rotoru dána vztahem
kde označení symbolem značí přidanou
soustavu, tedy vývažek . Podíl vývažku na vyšší tvary
kmitu, které nejsou vyvažovány, je opět zanedbatelný. Tzv. rezidua jsou
zanedbána.
Pak platí vztah
Tuto rovnici lze upravit do tvaru
pro i=1,2,3 ... p
Pro přidanou soustavu je
Optimální vyvážení i-tého tvaru kmitu bude, když je
pro každý tvar kmitu, tedy pro každé i.
V této rovnici pro i-tý tvar kmitu a přidané závaží pro m-tý tvar je
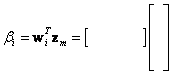
kde 
je dovažovací závaží pro m
– tý tvar kmitu. Jestliže se vyvažuje i-tý
tvar kmitu, další tvary kmitu nemohou být
rozváženy, proto musí být
V podstatě musí být vyvažování i-tého tvaru kmitu afinní vzhledem k m-tému tvaru kmitu. Afinní znamená kolmé. To znamená, že změna nevývahy pro i-tý tvar kmitu nesmí narušit (rozvážit) m-tý tvar kmitu.
Dále se chce, aby byla citlivost vyvažování pro všechny tvary kmitu stejná. Pak také platí soustava rovnic ve tvaru
Pak pro všechny přidané vývažky a pro všechny vyvažované tvary kmitu je
Nebo v maticovém tvaru
Odtud
kde 
udává rozložení vývažků pro p
tvarů kmitání v p rovinách.
Je to tzv. modální nevývaha. Skutečná velikost nevývažků musí být v souladu s měřenou odezvou v daných místech na rotoru. Odezva na rotoru v měřených místech na tzv. jednotkou modální nevývahu je dána vztahem
kde představuje matici dynamických
poddajností.
Skutečnou nevývahu je pak nutno korigovat na základě skutečně změřené odezvy při daných otáčkách.
Matici 
lze stanovit také experimentálně.
Poznámka
Metoda experimentálního stanovení koeficientů vlivu (matice )
Rovnici pro odezvu lze také přepsat do tvaru
kde 
je změřená odezva pro známou
nevývahu 
.
Odtud lze stanovit koeficienty příčinkových koeficientů. Metoda je založena na
principu stanovení každého koeficientu zvlášť, kdy se stanoví odezva
v místě i, jestliže se přidá závaží do místa j. Celkem je
potřeba provést celkem 
měření při stejných otáčkách,
jestliže se vyvažuje p tvarů kmitání použitím p vyvažovacích
rovin.