5. Redukce počtu stupňů volnosti

 

 

Metody redukce

 

Poznámka: Přímá a fyzikální zde není uvedena

 

·         Guyanova

·         Modální

·         Ve frekvenční oblasti

 

Guyanova redukce (tuhostní)

 

 

 

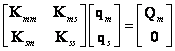
Z první rovnice

 

 

Z druhé rovnice

 

 

Potom

 

 

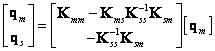
Odkud má transformační matice řádu  tvar

 

 

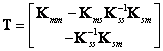
Pohybová rovnice po transformaci

 

 

Modální redukce

 

Modální transformace – transformace pohybové rovnice z fyzikálních souřadnic do hlavních

 

 

 

 

 - fyzikální souřadnice (mají rozměr)

 - hlavní (modální) souřadnice (bezrozměrné)

 

Po dosazení do pohybové rovnice a násobení zleva modální maticí levostranných vektorů

 

 

S využitím podmínek normy

 

 

Poznámky

·         Redukce matic spočívá v zahrnutí jenom určitého počtu vlastních vektorů.

·         Pro určitý typ matice tlumení je matice  diagonální a celý systém pohybových rovnic se rozpadá na nezávislé dif. rov. 1. řádu

 

Redukce ve frekvenční oblasti

 

Metoda dynamických poddajností - Základ je v syntéze „samostatných“ částí.

 

 

 

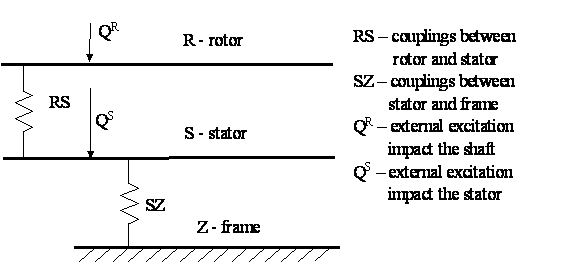
Scheme of rotor system

 

Matice dynamických poddajností „samostatného“ rotoru (obdobně „samostatného“ statoru)

Matice dynamických poddajností „samostatných“ vazeb

 

Rovnice rovnováhy a spojitostí posuvů

 

 

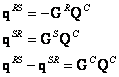
Nalezení vlastních čísel

 

 

Koaxiální hřídele

 

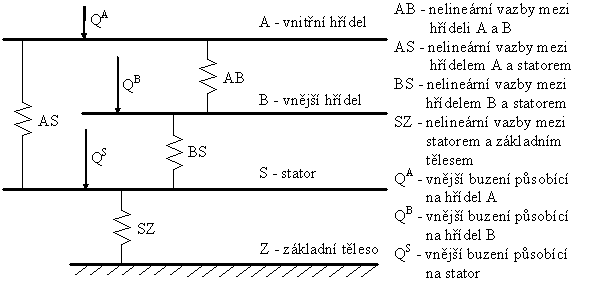Schéma rotorové soustavy

 

 

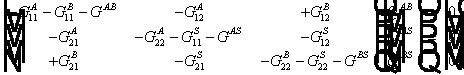
Poznámka – porovnání algoritmů DAMP a QRDAMP

DAMP	QRDAMP (účinnější - efficient)
1)      Lanczos – vytvoření třídiagonální matice H 2)      QR algoritmus k řešení problému vl. hodnot matice H	1)      Lanzcos – vytvoření třídiagonální matice netlumeného systému 2)      QR algoritmus pro řešení problému vl. hodnot netlumeného systému 3)      Modální redukce a transformace pohybových rovnic tlumeného systému do stavového prostoru 4)      QR algoritmus pro řešení problému vl. hodnot

© Ústav mechaniky těles, mechatroniky a biomechaniky
Admin e-mail: krejci.p@fme.vutbr.cz

Poslední aktualizace