Dynamika rotorových soustav
11. Dynamika rotačně periodických struktur - RPS
1. Řešení jako celek
Schéma části struktury je na obr. 1.
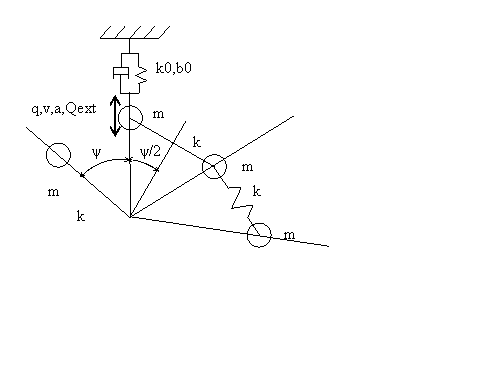
Obr. 1 Schéma části RPS
Předpokládejme, že počet rotačně periodických
struktur je 
.
Dále, že soustava kmitá 
uzlovými průměry.
Pro úhel 
Pro potenciální energii pružiny pak platí
kde
Obdobně pro zatlumenou funkci
Pohybová rovnice celé struktury má pak tvar
kde matice mají tvar
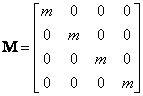
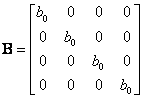
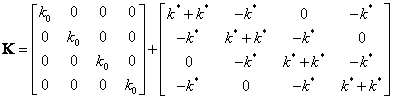
2. Řešení na základě vlastností RPS
Úplně uvolněná jedna struktura je na obr. 2.
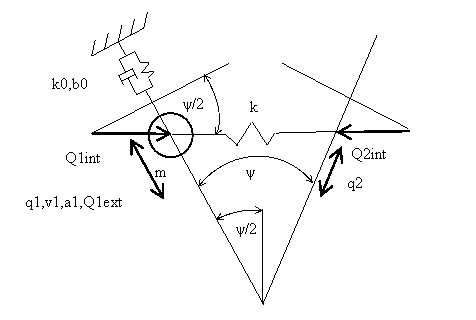
Obr. 2 Částečně uvolněná jedna struktura
Pro tuto strukturu lze psát pohybovou rovnici ve tvaru
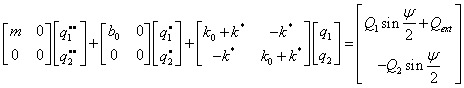
Fázové posunutí pohybujících se uzlů je dáno vztahem 
Pak platí
a také
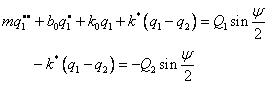
Pro předpokládané harmonické kmitání lze psát
Pak po dosazení
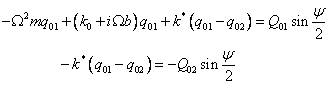
kde dále v druhé rovnici po úpravě je
a po dosazení do první rovnice
a další úpravou
a dále
odkud pro netlumenou soustavu
Odezva při vynuceném ustáleném kmitání
odkud
Odezva při přechodovém kmitání
Pro analýzu přechodového kmitání je možné použít tzv. „plný“ model.
Pro tuto strukturu lze psát pohybovou rovnici ve tvaru
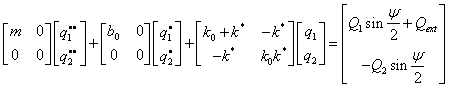
Fázové posunutí pohybujících se uzlů je dáno vztahem 
Pak platí
a také
Po dosazení
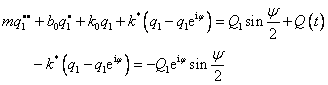
dosazením z druhé rovnice za 
Eulerovy vztahy
Což je pohybová rovnice pro řešení odezvy při přechodovém kmitání