 Dynamika rotorových soustav
Dynamika rotorových soustav
3. Kluzná a valivá ložiska
Dynamické vlastnosti kluzných ložisek
Poznámka 1
Analýza hydrodynamických tlumičů se od analýzy kluzných ložisek liší jedině v zahrnutí rotace u kluzných ložisek. U hydrodynamických tlumičů odpadá stacionární řešení.
Poznámka 2
Kavitace v kluzných ložiskách je v podstatě to, že nemůže existovat oblast se záporným tlakem oleje.
Poznámka 3
Dva přístupy k řešení
1. V časové oblasti (nekompletní řešení pro ustálené i přechodové kmitání)
2. Ve frekvenční oblasti (kompletní řešení ale pouze pro vynucené ustálené kmitání)
Je uveden teoretický přístup k analýze a přístup k výpočtovému modelování dynamických vlastností tenkých tekutinových vrstev. Je uvedeno porovnání řešení dle dvou přístupů. První přístup vychází z transformace, která má tvar konvolutorního integrálu. Pokud je tekutina stlačitelná, má tento přístup značné omezení. V takovém případě musí být pro separování pohybu tělesa a tekutiny použita jiná transformace. V tomto případě nemá transformace tvar konvolutorního integrálu. Ze závislostí komplexní dynamické síly na frekvenci buzení lze stanovit tenzory přídavných účinků.
Abstrakt
Interakce tělesa s tekutinou je jednou z nejčastějších případů vyskytujících se v praxi. Konkrétní technickou aplikací na kterou je zaměřen příspěvek, je interakce tuhého tělesa s tenkým tekutinovým filmem. Konkrétními případy pak jsou kluzná ložiska, hydrodynamické tlumiče, těsnící spáry atd. Aplikace se tedy týká dynamiky rotorových soustav. Z pohledu výpočtového modelování dynamických vlastností rotorových soustav jsou dva základní přístupy pro zahrnutí tekutinových subsystémů.
První přístup je založen na předpokladu řešení obou soustav jako vázané úlohy. Podstatou je stanovení silového účinku od tekutinového filmu na základě známých kinematických veličin hřídelové části. Matematický model tekutinového systému musí být co možná nejjednodušší, aby si komplexní řešení nevyžadovalo velké nároky na výpočtové časy. Nejpoužívanější rovnicí popisující dynamické vlastnosti tekutinového filmu je zde Reynoldsova rovnice. Snaha po co možná nejednodušším matematickém modelu vedla k řadě zjednodušující předpokladů.
Druhý přístup je založen na vzájemné separaci obou soustav. Pro daný parametr hřídelové části (zpravidla poloha středu hřídele) se stanoví databáze přídavných účinků. Tyto jsou pak při řešení dynamických vlastností celé rotorové soustavy přidávány k hřídelové části na levou stranu pohybové rovnice, k maticím hmotnosti, tlumení a tuhosti.
Vhodnou transformací lze vzájemně separovat pohyb tělesa a tekutiny. Transformace má tvar konvolutorního integrálu. V tomto případě jsou přídavné účinky od tekutiny závislé pouze na poloze středu hřídele. Výchozími rovnicemi pro analýzu dynamických účinků jsou Navier – Stokesova rovnice, rovnice kontinuity a okrajové podmínky. Takto stanovené přídavné účinky lze použít při stacionární i nestacionární analýze. Není učiněn žádný předpoklad na pohyb středu hřídele. Při použití této transformace je pak tlak závislý nejen na rychlosti, ale i na zrychlení pohybu středu hřídele.
Pokud je tekutina stlačitelná, nebo je analyzován případ kavitujících ložisek, má tento přístup značné omezení. V takovém případě musí být pro separování pohybu tělesa a tekutiny použita jiná transformace. Ta vychází z předpokladu harmonického buzení a tudíž i předpokládané harmonické odezvy. Transformace nemá tvar konvolutorního integrálu.
Oproti předchozímu případu je zde jisté omezení. Dynamické síly působící na hřídel jsou opět závislé pouze na poloze středu hřídele, avšak rovněž na frekvenci vnějšího buzení rotorové soustavy, obecně nezávislé na otáčkách. Ze závislostí komplexní dynamické síly na frekvenci buzení lze stanovit tenzory přídavných účinků.
Je uveden teoretický přístup k analýze a přístup k výpočtovému modelování. Analýza je doplněna řešením modelové úlohy a je uvedeno porovnání řešení dle obou přístupů. Jsou uvedeny rovnice pro aplikaci metody sítí i metody kontrolních objemů.
Úvod
V prvním přístupu se oba systémy řeší jako vázaná úloha. Podstatou je stanovení silového účinku od tekutinového filmu na základě známých kinematických veličin hřídelové části. Matematický model tekutinového systému musí být co možná nejjednodušší, aby si komplexní řešení nevyžadovalo velké nároky na výpočtové časy. Nejpoužívanější rovnicí popisující dynamické vlastnosti tekutinového filmu je zde Reynoldsova rovnice, která je uvedena např. v [1]. Odvození sil od tekutiny působící na hřídel pro stanovení tenzorů přídavných účinků je uvedeno např. v [3 - 5].
Druhý přístup je založen na vzájemné separaci obou soustav. Pro daný parametr hřídelové části (zpravidla poloha středu hřídele) se stanoví databáze přídavných účinků. Tyto jsou pak při řešení dynamických vlastností celé rotorové soustavy přidávány k hřídelové části na levou stranu pohybové rovnice, k maticím hmotnosti, tlumení a tuhosti. V tomto přístupu je nutno nalézt pro separaci vhodnou transformaci.
Pro nestlačitelnou tekutinu má transformace tvar konvolutorního integrálu (viz [6]). V tomto případě jsou přídavné účinky od tekutiny závislé pouze na poloze středu hřídele. Pokud je tekutina stlačitelná, nebo je analyzován případ kavitujících ložisek, má tento přístup značné omezení a musí se použít jiná transformace. Ta vychází z předpokladu harmonického buzení a také harmonické odezvy a nemá tvar konvolutorního integrálu. Dynamické síly působící na hřídel jsou opět závislé pouze na poloze středu hřídele, avšak rovněž na frekvenci vnějšího buzení rotorové soustavy. Ze závislostí komplexní dynamické síly na frekvenci buzení lze stanovit tenzory přídavných účinků.
V příspěvku je uveden teoretický základ k analýze a přístup k výpočtovému modelování. Analýza je doplněna řešením modelové úlohy a je uvedeno porovnání řešení dle obou přístupů.
Teoretický základ k novému přístupu pro nestlačitelnou tekutinu je uveden v [6]. V [7] je uvedeno srovnání Reynoldsovy a Navier – Stokesovy rovnice pro dlouhé nekavitující kluzná ložiska. Přístup k výpočtovému modelování statických i dynamických vlastností nekavitujících kluzných ložisek je uveden v [7 a 8]. Pro aproximaci řešení i pro popis oblasti vyplněné tekutinou je použito Bézierovo těleso [7].
Pro prostorový model
lze specifikovat dva typy okrajových podmínek na čelech kolmých na osu hřídele.
V první podmínce, která je označena ![]() , se zadávají rychlosti a tlaky se
počítají, ve druhé, která je označena
, se zadávají rychlosti a tlaky se
počítají, ve druhé, která je označena ![]() , se zadávají tlaky a rychlosti se
počítají. Na základě sil od tekutiny, které působí na hřídel lze určit tenzory
přídavných účinků při stacionárním i nestacionárním řešení. Ty jsou závislé
pouze na jednom parametru, kterým je poloha středu hřídele.
, se zadávají tlaky a rychlosti se
počítají. Na základě sil od tekutiny, které působí na hřídel lze určit tenzory
přídavných účinků při stacionárním i nestacionárním řešení. Ty jsou závislé
pouze na jednom parametru, kterým je poloha středu hřídele.
Aplikace Reynoldsovy rovnice - stávající přístup

Coordinate frames and bearing properties
![]()
Kluzná ložiska
![]()
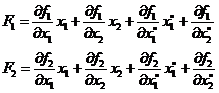
Přídavná hmotnost se stanoví na základě předpokladu, že rychlostí profil nehmotné tekutiny a s jejím zahrnutím jsou stejné. Prvky matice potom z kinetické energie.
Navier – Stokesova rovnice – nový přístup
Výpočtové modelování v časové oblasti
![]()
Rovnice kontinuity
![]()
Okrajové podmínky
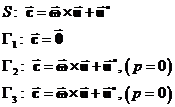
S využitím Einsteinovy sumační symboliky je
Navier – Stokesova rovnice
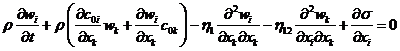
Rovnice kontinuity
![]()
Okrajové podmínky
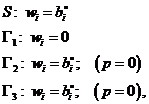
kde
![]()
Transformace
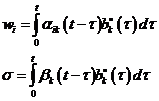
Po dosazení
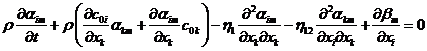
![]()
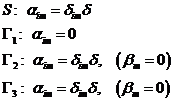
Přídavná hmotnost
![]()
Přídavné tlumení
![]()
Přídavná tuhost
![]()
Výpočtové modelování ve frekvenční oblasti
Teoretický rozbor
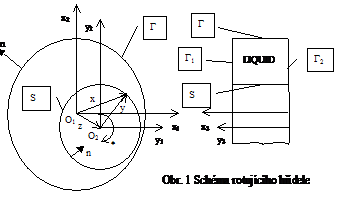
Na obr. 1 je
nakreslen příklad kluzného ložiska. V pevném nerotujícím souřadnicovém
systému je poloha středu hřídele označena počátkem O2. Kolem tohoto
středu, který je dán souřadnicemi ![]() rotuje hřídel úhlovou rychlostí
rotuje hřídel úhlovou rychlostí ![]() . Pro reálnou
tekutinu jsou na površích rychlosti tekutiny a tělesa stejné. V textu je
použita Einsteinova sumační symbolika. Výchozí rovnice pro analýzu jsou Navier
– Stokesova, kontinutity a okrajové podmínky ve tvaru
. Pro reálnou
tekutinu jsou na površích rychlosti tekutiny a tělesa stejné. V textu je
použita Einsteinova sumační symbolika. Výchozí rovnice pro analýzu jsou Navier
– Stokesova, kontinutity a okrajové podmínky ve tvaru
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
V případě aplikace metody kontrolních objemů lze rovnice (1) a (2) přepsat do integrálního tvaru.
![]() (4)
(4)
![]() (5)
(5)
Pro řešení lze dále předpokládat, že jak poloha středu hřídele, tak i rychlost a tlak jsou dány součtem stacionární a nestacionární části ve tvaru
![]() (6)
(6)
Stacionární řešení
Vzhledem k tomu, že stacionární části nejsou funkcí času, mají rovnice (4) a (5) tvar
![]() (7)
(7)
![]() (8)
(8)
a nebo v případě aplikace metody kontrolních objemů mají tvar
![]() (9)
(9)
![]() (10)
(10)
Okrajové podmínky jsou v tomto případě takové, že rychlost tekutiny a tělesa na površích (např. na hřídeli) stejné, tedy
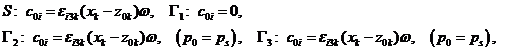 (11)
(11)
Cílem stacionárního řešení je nalezení staticky rovnovážné polohy a stanovení rychlostního a tlakového pole.
Nestacionární řešení
V dalším bude analyzován velmi častý případ v technické praxi, kdy buzení i odezva jsou harmonickými funkcemi ve tvaru
![]() (12)
(12)
To je případ řešení odezvy při vynuceném ustáleném kmitání. I v tomto případě lze vhodnou transformací vyloučit neznámou rychlost středu hřídele z okrajových podmínek, které mají tvar
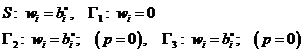 (13)
(13)
kde ![]() . Pak také lze pro
rychlosti a tlaky předpokládat řešení ve tvaru
. Pak také lze pro
rychlosti a tlaky předpokládat řešení ve tvaru
![]() (14)
(14)
Po dosazení mají hlavní rovnice tvar
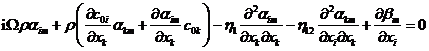
![]() (15)
(15)
nebo v případě aplikace metody kontrolních objemů
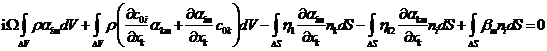 (16)
(16)
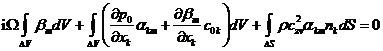 (17)
(17)
![]() (18)
(18)
Pro sílu od tekutiny působící na hřídel platí vztah
![]() (19)
(19)
a dále po dosazení (14)
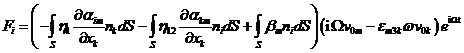 (20)
(20)
kde výraz v závorce lze zapsat ve tvaru
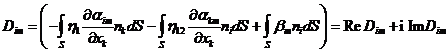 (21)
(21)
S ohledem na rovnici popisující pohyb hřídele lze výslednou matici dynamické tuhosti tekutinového filmu napsat jako součet dvou členů. První člen je úměrný rychlosti pohybu hřídele a druhý člen je úměrný její poloze. Pak pro sílu od tekutiny působící na hřídel platí vztah
![]() (22)
(22)
První člen straně představuje dynamické tlumení a druhý dynamickou tuhost. Obě matice jsou komplexní a mají tvar
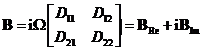 (23)
(23)
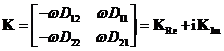 (24)
(24)
Na základě řady
výpočtových analýz modelových úloh jsou závislosti reálné a imaginární části
všech prvků matic dynamických
tuhostí ![]() dle obr. 2. Závislost imaginární
části prvků matice
dle obr. 2. Závislost imaginární
části prvků matice ![]() na frekvenci se blíží lineární
závislosti, což znamená to, že tato část odpovídá tlumení od tekutinového filmu
a není frekvenčně závislé. Závislost reálné
části prvků matice
na frekvenci se blíží lineární
závislosti, což znamená to, že tato část odpovídá tlumení od tekutinového filmu
a není frekvenčně závislé. Závislost reálné
části prvků matice ![]() na frekvenci se blíží kvadratické
závislosti, což svědčí o tom, že tato část odpovídá přídavné
hmotnosti a není frekvenčně závislá. Závislost
imaginární části prvků matice
na frekvenci se blíží kvadratické
závislosti, což svědčí o tom, že tato část odpovídá přídavné
hmotnosti a není frekvenčně závislá. Závislost
imaginární části prvků matice ![]() na frekvenci se blíží lineární
závislosti, což znamená to, že i tato část odpovídá tlumení od tekutinového filmu
a není frekvenčně závislé. Závislost reálné části prvků matice
na frekvenci se blíží lineární
závislosti, což znamená to, že i tato část odpovídá tlumení od tekutinového filmu
a není frekvenčně závislé. Závislost reálné části prvků matice ![]() není frekvenčně
závislé a odpovídá tuhosti tekutinového filmu.
není frekvenčně
závislé a odpovídá tuhosti tekutinového filmu.
Modelová úloha
Jako modelová úloha
bylo zvoleno ložisko s parametry ![]() ,
, ![]() ,
, ![]() a
a ![]() . Fyzikální veličiny tekutiny jsou
. Fyzikální veličiny tekutiny jsou ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Statická
poloha středu hřídele byla uvažována v polovině radiální mezery ve
vodorovném směru (osa
. Statická
poloha středu hřídele byla uvažována v polovině radiální mezery ve
vodorovném směru (osa ![]() ). Relativní dynamická poloha byla
měněna v rozsahu 0.0 – 0.6 ve vodorovném směru. Frekvence buzení pro
výpočet frekvenčně závislé tuhosti byla uvažována v rozsahu 0 – 1000
s krokem 250 rad/s. Přídavné účinky od tekutiny byly následně stanoveny
pro frekvenci shodnou s otáčkovou. Vztahy pro výpočet bezrozměrných
veličin jsou vzaty z [3 - 5].
). Relativní dynamická poloha byla
měněna v rozsahu 0.0 – 0.6 ve vodorovném směru. Frekvence buzení pro
výpočet frekvenčně závislé tuhosti byla uvažována v rozsahu 0 – 1000
s krokem 250 rad/s. Přídavné účinky od tekutiny byly následně stanoveny
pro frekvenci shodnou s otáčkovou. Vztahy pro výpočet bezrozměrných
veličin jsou vzaty z [3 - 5].
V příspěvku je uveden teoretický základ analýzy v časové i frekvenční oblasti. Proto jsou pro porovnání uvedeny některé výsledky výpočtového modelování s využitím obou přístupů. Vlastní analýza je zaměřena na porovnání přídavných účinků dlouhého ložiska (v obrázcích (3-5) označeno „long“) v časové a frekvenční oblasti. Pro porovnání byl vybrán pouze prvek (1,1). Na obr. 3-5 jsou nakresleny závislosti hmotnosti, tlumení a tuhosti dlouhého ložiska stanovené z řešení v časové a frekvenční oblasti. Závislosti přídavných účinků stanovených v časové oblasti jsou v obrázcích označeny „time“ a závislosti stanovené ve frekvenční oblasti jsou označeny „frek“.
Závěr
S pohledu na nový matematický model i s ohledem na nový přístup k výpočtovému modelování lze učinit následující závěry:
· Na základě transformací lze vzájemně separovat pohyb tělesa (hřídele) a tekutiny. Přídavné účinky (tenzory přídavných hmotností, tlumení a tuhosti) jsou závislé pouze na jednom parametru, kterým je poloha středu hřídele. Tento přístup umožňuje vytvoření databáze přídavných účinků pro daný typ ložiska.
· Přídavná hmotnost, tlumení i tuhost nejsou frekvenčně závislé na frekvenci vnějšího buzení.
· Uvedený přístup k řešení lze bez problémů rozšířit na hydrodynamické tlumiče, nebo těsnící spáry.
· Aplikace Bézierova tělesa obecně umožňuje rozšíření i na ložiska s jiným tvarem vnější nerotující oblasti, například přesazená, nebo citrónová, obecně (n-lobe bearings).
· Aplikace Bézierova tělesa rovněž umožňuje zahrnout jiný typ okrajových podmínek pro rychlosti a tlaky, např. specifikovat přívod oleje do ložiska (servofluidní ložiska).
· Lze analyzovat i axiální kluzná ložiska
Na základě analýzy modelových úloh lze učinit následující závěry:
· U přídavné hmotnosti i tlumení je dosažena dobrá shoda při řešení v časové i frekvenční oblasti.
· Podstatnější rozdíl je v dynamické tuhosti. Větších hodnot nabývá tuhost stanovená v časové oblasti. To může být zapříčiněno rozdílnými výpočtovým modely.
Literatura
[1] Krämer, E., Dynamics of Rotors and Foundations, Springer Verlag, New York, 1993.
[2] Vance, J., M., Rotordynamics of Turbomachinery, Wiley, New York, 1988.
[3] Crandal, S., H., El-Shafei, A., Momentum and Energy Approximations for Elementary Squeeze Film Damper Flows, ASME Journal of Applied Mechanics, Vol. 60(3), pp. 728 - 736, 1993.
[4] El-Shafei, A., Unbalance Response of a Jeffcott Rotor Incorporating Long Squeeze Film Dampers, ASME Journal of Vibration and Acoustics, Vol. 113(11), pp. 85 - 94, 1991.
[5] El-Shafei, A., Modelling Fluid Inertia Forces of Short Journal bearings for Rotodynamics Applications, Transactions of the ASME, Journal of Vibrations and Acousttics. Vol. 117, pp. 462 - 469, 1995.
[6] Pochylý, F, at all, The nonstationary Motion of the Rigid Body in Real Liquid, Proc. of 3rd International Conference Engineering Aero-Hydroelasticity, Prague, pp. 346 - 351, 1999.
[7] Malenovský, E., Pochylý, F., Some Results of Computational Modelling of Dynamic Behaviours of Journal Bearings by the Bézier Body Application, Journal of Mechanical Engineering, Vol. 52(4), pp. 235 - 258, 2001.
[8] Malenovský, E., Pochylý, F., Computational Modelling of Dynamic Properties of Long Journal Bearings by Using the Bézier Body. Proc. of Fünfte Internationale Tagung Schwingungen in Rotierenden Maschinen. Institut für Maschinendynamik und Messtechnik. Technische Universtät Wien, Wien, Austria, pp. 13 - 20, 2001.
[9] Malenovský, E., Pochylý, F., Comparison of Dynamic Behaviour of SQUEEZE Film Dampers Calculated Using Reynolds and Navier-Stokes Equations, Proc., of Fifth World Congress on Computational Mechanics, http: Vienna, Austria, pp. 1 - 10, 2002.
[10] Malenovský, E., Pochylý, F., Some Results of Computational Modelling of the Dynamic Behaviour of SQUEEZE Film Dampers Using Reynolds and Navier-Stokes Eqs., Proc. of Fifth European Conference on Structural Dynamics EURODYN 2002, Munich, Germany, pp. 729 - 734, 2002.
[11] Pochylý, F., Malenovský, E., The Comparison of Pressure and Velocity Fields of SQUEEZE film Dampers Calculated by the Reynolds and Navier-Stokes Equations, Proc. of Sixth International Conference on Rotor Dynamics, Sydney, Australia, pp. 541 - 548, 2002.
[12] Malenovský, E., Pochylý, F.: Computational modelling of the dynamic behaviour of compressible fluid film - rigid body interaction using the Bézier body. Proc. of 6. tagung Schwingungen in Rotierenden Maschinen, Darmstadt, Germany, pp. 255 – 262, 2003.
[13] Malenovský, E., Pochylý, F.: The Comparison of Additional Effects of Journal Bearings Calculated Using the Reynolds and Navier-Stokes Equations. Proceedings of the 11th World Congress in Mechanism and Machine Science. April 1 – 4, 2004, Tianjin, China, 2004, p. 1 – 5.
 Seznam použitého
označení:
Seznam použitého
označení:
![]() -délka ložiska,
-délka ložiska, ![]() -
-![]() tá část
kovariantního normálového vektoru,
tá část
kovariantního normálového vektoru, ![]() -tlak,
-tlak, ![]() -poloměr hřídele a
ložiska,
-poloměr hřídele a
ložiska, ![]() -čas,
-čas,
![]() -rychlosti,
-rychlosti,
![]() -souřadnice
středu hřídele,
-souřadnice
středu hřídele, ![]() -souřadnice,
-souřadnice, ![]() -funkce rychlosti,
-funkce rychlosti, ![]() -funkce tlaku,
-funkce tlaku, ![]() -hustota,
-hustota, ![]() -Levi – Civitův
tenzor,
-Levi – Civitův
tenzor, ![]() -bezrozměrná
poloha středu hřídele,
-bezrozměrná
poloha středu hřídele, ![]() -úhlová rychlost rotace hřídele,
-úhlová rychlost rotace hřídele, ![]() -frekvence
buzení,
-frekvence
buzení, ![]() -hmotnost,
-hmotnost,
![]() -
tlumení,
-
tlumení, ![]() -tuhost,
-tuhost,
![]() -dynamická
viskozita,
-dynamická
viskozita, ![]() -druhá
viskozita,
-druhá
viskozita, ![]() -rychlost
zvuku,
-rychlost
zvuku, ![]() -dynamická
síla od tekutinového filmu,
-dynamická
síla od tekutinového filmu, ![]() -imaginární jednotka,
-imaginární jednotka, ![]() -kontrolní
objem,
-kontrolní
objem, ![]() -kontrolní
plocha.
-kontrolní
plocha. ![]() -vnitřní
povrch,
-vnitřní
povrch, ![]() -vnější
povrch,
-vnější
povrch, ![]() -plocha
čel,
-plocha
čel, ![]() ,
index 0 značí statickou analýzu, nebo amplitudy řešení.
,
index 0 značí statickou analýzu, nebo amplitudy řešení.
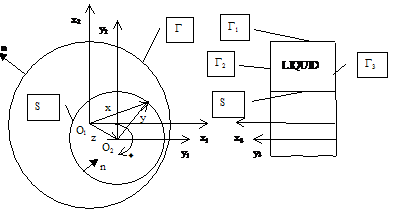
Obr. 1 Schéma kluzného ložiska

Obr. 2 Závislosti dynamických tuhostí na frekvenci
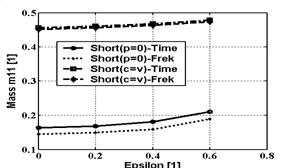
Obr. 3 Hmotnost dlouhého ložiska
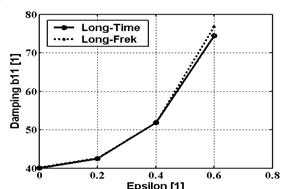
Obr. 4 Tlumení dlouhého ložiska
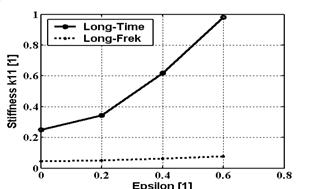
Obr. 5 Tuhost dlouhého ložiska
Hydrodynamický tlumič
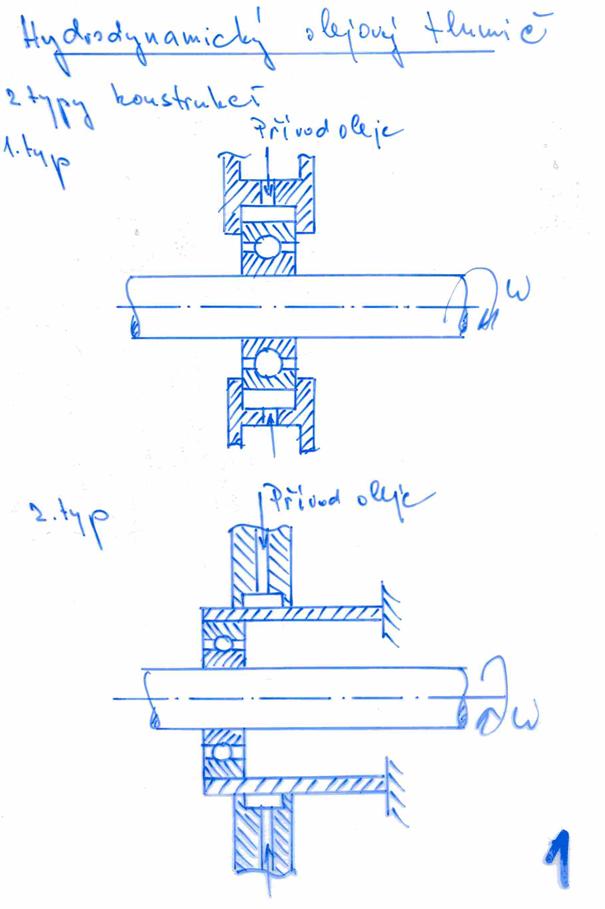
Dynamické vlastnosti valivých ložisek
