Dynamika rotorových soustav
8. Metody řešení dynamických vlastností rotorových soustav
odezva při přechodovém
I při řešení odezvy při přechodovém kmitání byla jako základní využita Aitkenova a Newtonova-Raphsonova metoda. Vnější buzení může mít charakter quasi stacionárního, při kterém se nemění otáčky rotorové soustavy, případně mohou být otáčky časově závislé. Ve druhém případě může být řešena výpočtová simulace např. přejezdu přes rezonanci se zadaným zrychlením.
Pro řešení úloh na bázi MKP je možné sestavit pohybovou rovnici s nelinearitami na levé, případně na pravé straně. Prvotní specifikace nelineárních vazebných prvků je dána jejich silovou funkční závislostí na časově závislých parametrech. V případě stanovení přídavných účinků ve tvaru matic hmotnosti, tlumení, nebo tuhosti se tyto stanoví příslušnými parciálními derivacemi funkčních závislostí na základě Taylorova rozvoje funkce. Pro mnohé vazby, např. hydrodynamické tlumiče, nebo kluzná ložiska jsou silové funkční závislosti značně složité a provedení derivací v analytickém tvaru je téměř nemožné. Proto se stanovují numericky na základě malých perturbací výchylek a rychlostí. Aitkenova metoda umožňuje zahrnout oba případy zadávání nelineárních funkcí, pro Newtonovu-Raphsonovu metodu je výhodnější přístup s maticemi, při konstantní pravé straně v daném kroku řešení.
Základní přehled metod
Výsledek – časově závislá odezva při buzení v daném časovém rozsahu. Může se provádět i výpočtová simulace startu na dané otáčky při specifikovaném zrychlení.
Označení - 
je časový krok řešení
Metody přímé integrace pohybových rovnic
·
- explicitní (Diferenční, R-K) -
·
- implicitní (Newmarkova, R-K) -
Metody Runge-Kuttovy (R-K) - explicitní
- implicitní
Řešení diferenciální rovnice
odkud
Podstata metod
kde 
- jsou konstanty
- funkční
hodnoty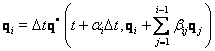 
Metoda druhého řádu
Metoda třetího řádu
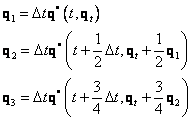
Metoda čtvrtého řádu
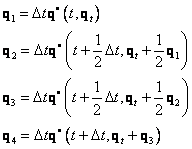
Metoda centrálních diferencí
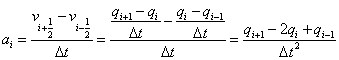
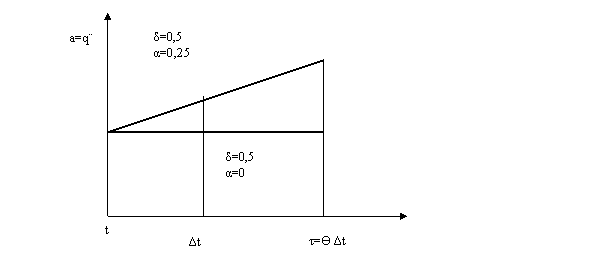
Newmarkova metoda
Modální transformace (redukce)
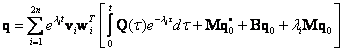
Redukce ve frekvenční oblasti
Matice pro „samostatný“ rotor, nebo stator
Matice pro vazby
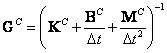
Výsledný tvar matic
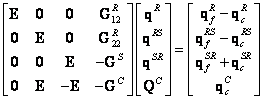
Nelineární úlohy
a) Aitkenova metoda v kombinaci s MKP
Pohybová rovnice (obecně i s nelineárními přídavnými účinky zahrnutými do matic hmotnosti, tlumení a tuhosti) má tvar
(19)
Pro
řešení diferenciální rovnice lze aplikovat některou z známých explicitních,
případně implicitních metod řešení. V našem případě byla použita Newmarkova
metoda, přičemž výsledný tvar soustavy algebraických rovnic pro řešení výchylky
v kroku „
+1“
při zahrnutí nelinearit na levé straně má pohybová rovnice má na začátku
iterace tvar
(20)
Při aplikaci tříkrokové metody je posloupnost výpočtových kroků následující
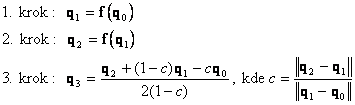(21)
Pro
dosažení požadované přesnosti lze použít několik přístupů. Doposud se nejlépe
osvědčil přístup, kdy norma přírůstku deformace 
je menší, než určitá procentuální
hodnota normy výchylky v kroku 3.
b) Newtonova - Raphsonova metoda v kombinaci s MKP
Jednou z možností jak zjednodušit algoritmus s cílem neprovádět sestavování Jacobiho matice parciálních derivací je převedení nelineárních členů ve tvaru přídavných matic hmotnosti, tlumení a tuhosti na levou stranu pohybové rovnice. V dalším budou uvedeny tři možné přístupy k řešení.
1. Přístup
Algoritmus
je podobný jako pro řešení vynuceného ustáleného kmitání. Vychází z aplikace
Newmarkovy metody (viz [13], odkud i koeficienty 
) při řešení diferenciálních
rovnic. Algoritmus řešení odezvy v kroku „“ jsou následující:
1.
Krok - Výpočet výchylky 
z rovnice
(22)
nebo zkráceně
(23)
kde
horní index „
“
značí efektivní matice a dolní indexy značí časový krok ze kterého se dosazují
příslušné kinematické veličiny.
2. Krok - Výpočet vektoru „nevyrovnaných“ vnitřních sil podle vztahu
(24)
Dále se vypočítá přírůstek deformace od „nevyrovnaných“ sil
(25)
Nová výchylka v
kroku „“
pak je
. (26)
Iterační cyklus v kroku 2 pokračuje, pokud norma vektoru „nevyrovnaných“ sil není menší než určitá procentuální hodnota normy vektoru efektivního vnějšího zatížení.
2. Přístup
Algoritmus je podobný předcházejícímu a opět vychází z aplikace Wilsonovy - Q metody při řešení diferenciálních rovnic [13] a [14]. Pohybová rovnice v přírůstkovém tvaru je
(27)
kde
pro 
,
(při použití Newmarkovy-Wilsonovy metody pro 
a pokud je 
, obdrží se klasická
Newmarkova metoda) je
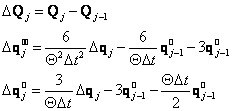(28)
Dosazením vztahů (28) do (27) se obdrží
(29)
kde
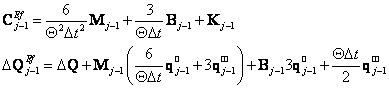(30)
Kinematické
veličiny v kroku „“ pak jsou
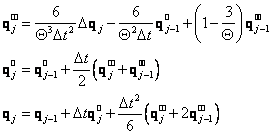(31)
Algoritmus řešení je pak následující
1. Krok: Pomocí rovnice (29) výpočet prvního odhadu přírůstku výchylky a dle vztahů
(27) výpočet přírůstku rychlosti a zrychlení, přičemž jako vstupní veličiny jsou
brány kinematické veličiny z předchozího kroku
2. Krok: Výpočet přírůstku nevyvážených efektivních sil dle vztahu
(32)
Řešení rovnice
(33)
Korekce
přírůstku výchylky v kroku „“
(34)
Iterace v kroku 2 pokračuje, dokud není přírůstek nevyvážených sil dostatečně malý.
3. Krok: Výpočet nových kinematických veličin, tj. přemístění, rychlosti a zrychlení v kroku
„“ dle vztahů (31).
3. Přístup
V tomto přístupu se jedná o aplikaci dvoukrokové iterace s lichoběžníkovým pravidlem. Pohybová rovnice (27) se přepíše do tvaru
(35)
1. Iterační krok : Výpočet následujících kinematických veličin
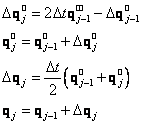(36)
dále se řeší soustava algebraických rovnic
(37)
a vypočítá se zrychlení
(38)
2. Iterační krok: Výpočet nových kinematických veličin
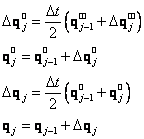(39)
Výpočet nového zrychlení (řešením soustavy algebraických rovnic) dle vztahu
(40)
a
následuje nový výpočet zrychlení v kroku „“
(41)
a výpočet nevyvážených setrvačných sil
(42)
Iterace pokračuje do té doby, pokud není přírůstek setrvačných sil dostatečně malý.
c) Aitkenova metoda v kombinaci s MM
Výchozí nelineární rovnice sestavená na bázi této metody (viz rov. (2.18), nebo (3.36)) má tvar
(43)
přičemž
vektor neznámých (výchylek i sil) v čase , v prvním iteračním cyklu se
vypočítá ze vztahu
(44)
I v tomto případě použijeme tříkrokovou metodu. Posloupnost výpočtových kroků je pak následující
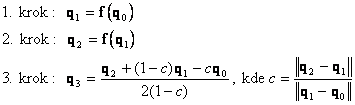(45)
Algoritmus řešení je tedy po formální stránce shodný s tím, který je uveden výše pro kombinaci s MKP. Rozdíl je ve třetím kroku, kde je nutno zvlášť provést výpočet pro část vektoru obsahujícího neznámé typu deformace a zvlášť pro část vektoru obsahujícího síly ve vazbách, včetně norem. Obdobným způsobem je nutno modifikovat výpočet v kritériu pro ukončení iteračního cyklu. Pro výpočet rychlosti a zrychlení lze použít vztahy pro diferenční, případně Newmarkovu metodu.
Algoritmus celkového řešení se skládá z těchto kroků
· Řešení problému vlastních hodnot „volného“ rotoru, na základě kterého se sestavuje matice „poddajnosti“ GR.
· Řešení problému vlastních hodnot „volného“ statoru, na základě kterého se sestavuje matice „poddajnosti“ GS. Tuto lze rovněž sestavit na základě experimentálně stanovených modálních vlastností.
· Řešení odezvy při přechodovém kmitání
„volného“ rotoru, na základě kterého se sestavuje vektor 
.
· Řešení odezvy při přechodovém kmitání
„volného“ statoru, na základě kterého se sestavuje vektor 
.
· Sestavení matice soustavy a vektoru pravé strany. Následuje její řešení včetně iterace, přičemž se po každé iteraci vypočítávají nové rychlosti a zrychlení. Iterační cyklus končí, když rozdíl příslušných výchylek a vazbových sil mezi prvním a třetím krokem řešení je dostatečně malý.
d) Newtonova - Raphsonova metoda v kombinaci s MM
Algoritmus
této metody je následující. Označíme-li matici soustavy G, .vektor
neznámých veličin q a pravou stranu rovnice Q (viz rov. (2.18),
nebo (3.19)), má výchozí rovnice na začátku iteračního cyklu v časovém
kroku tvar
(46)
V druhém kroku (ten již je součástí iteračního cyklu) se zjistí vektor „nevyrovnaných“ vnitřních neznámých veličin, který zahrnuje i nevyrovnané výchylky i síly podle vztahu
(47)
Dále se vypočítá přírůstek výchylky a vazbových sil od nevyrovnaných výchylek a sil
(48)
a
nová výchylka a vazbové síly v kroku „“
. (49)
Pro výpočet rychlosti a zrychlení lze použít vztahy pro diferenční, případně Newmarkovu metodu. S ohledem na to, že vektor neznámých obsahuje výchylky i síly, je nutno modifikovat výpočet v kritériu pro ukončení iteračního cyklu, který pokračuje, až vektor nevyrovnaných sil je v nějakém vhodném měřítku dostatečně malý.
Poznámky k řešení přechodového kmitání
V tomto případě má MM ve srovnání s klasickou MKP následující rozdíly:
· Matice G není matice dynamických tuhostí, která je nutná pro výpočet deformací.
· Vektor vnitřních sil nevyjadřuje vnitřní síly v soustavě.
· Pravá strana rovnice (46) má tvar, který vyplývá z aplikace metody dynamických poddajností, tedy obsahuje výchylky volných podsystémů.
· Z řady provedených výpočtů nelineárních úloh rotorových soustav se více osvědčila klasická Newton-Raphsonova metoda, ve srovnání s modifikovanou, stejně jako u MKP.
· Všechny navržené algoritmy byly autorem softwarově zpracovány a otestovány. Z řady provedených výpočtů nelineárních modelových úloh rotorových soustav i úloh technické praxe se více osvědčila klasická Newton-Raphsonova metoda, ve srovnání s modifikovanou.
·
Při iteračním výpočtu podle
kteréhokoliv přístupu (MKP i MM) je zásadní otázka, zda sestavovat nové matice
i s rychlostí stanovenou v daném kroku řešení, nebo ponechat rychlost
z předchozího kroku a měnit pouze výchylku. Pro některé případy
nelineárních funkcí docházelo při zahrnutí změny výchylky i rychlosti
v jednom kroku iterace ke ztrátě numerické stability řešení. Např. pro
případ kluzných ložisek s relativní polohou středu hřídele 
blízkou jedné.
Mohou tak vzniknout tři algoritmy pro sestavení vnitřního iteračního cyklu.
1. Algoritmus
Při iteracích se mění současně všechny kinematické veličiny.
2. Algoritmus
Při iteracích se mění pouze výchylka a rychlost i zrychlení se nemění. Teprve po ukončení iterování výchylek, nastává změna rychlosti a v iterační cyklus se pokračuje. Po ukončení iterování rychlostí nastává změna zrychlení.
3. Algoritmus
Při iteracích se současně mění výchylka i rychlost a zrychlení se nemění. Teprve po ukončení iterování výchylek a rychlostí, nastává změna zrychlení.
Na základě testování všech tří algoritmů nelze učinit jednoznačný závěr, který je nejvýhodnější, resp. který vykazuje největší numerickou stabilitu pro nejširší okruh nelinearit. Vhodnost algoritmu závisí do značné míry na typu nelineární funkce, zejména na změnu které kinematické veličiny je funkce nejvíce citlivá. Velký vliv má i velikost časového kroku.