Dynamika rotorových soustav

2. Campbellův diagram

Definice

Obecně je to závislost vlastních frekvencí na parametru. V rotorových soustavách jsou tímto parametrem otáčky hřídele.

Úvod

Vlastní čísla

- systém je nestabilní

- systém je stabilní

Campbellův diagram – závislost na úhlové rychlosti rotace hřídele

Tři případy

1. Bez gyroskopických účinků a symetrické uložení hřídele

2. S gyroskopickými účinky a symetrickým uložením hřídele

3. S gyroskopickými účinky a nesymetrickým uložením hřídele

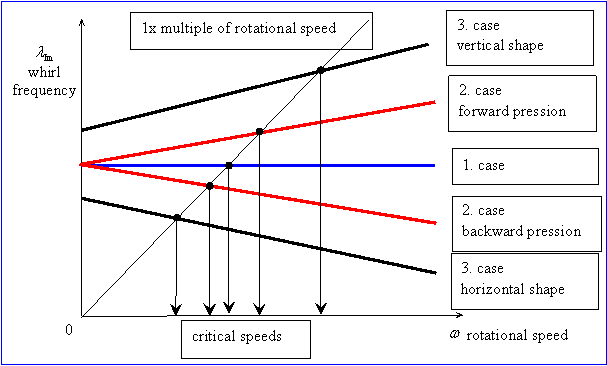
Zobrazení Campbellových diagramů

Úhlové rychlosti

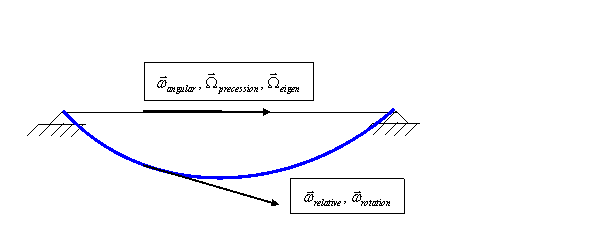
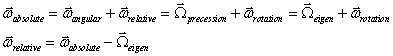
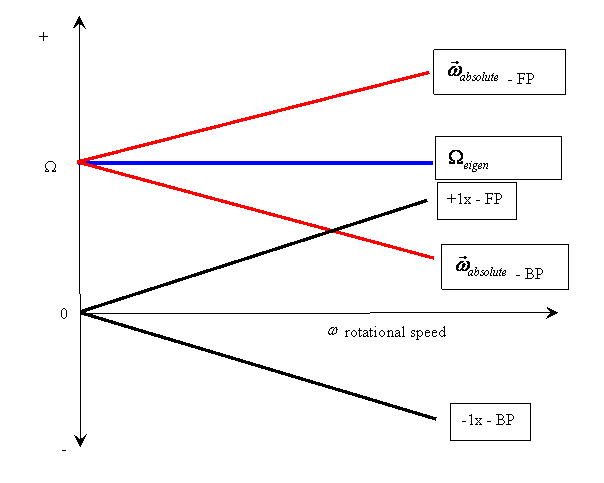
Absolute system

Tlumení v rotorových soustavách

Pohybová rovnice

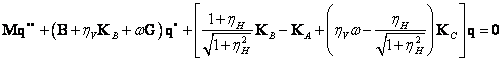
Modely tlumení

· Vnější

· Materiálové viskozní

· Materiálové hysterezní

· Proporcionální

Hysterezní materiálové tlumení

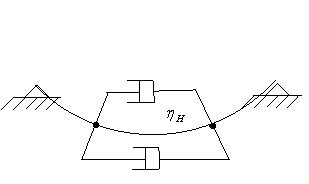
Model

Viskozní materiálové tlumení

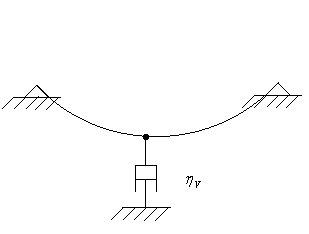
Model

Proporcionální tlumení

Experimentální stanovení koeficientů proporcionálního tlumení

pro j-tý tvar kmitu

- hlavní (modální) tlumení

- hlavní (modální) hmotnost

- hlavní (modální) tuhost

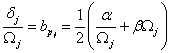
Tři případy stanovení koeficientů proporcionálního tlumení:

· zná se pouze frekvence a tlumení jednoho tvaru

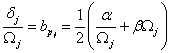
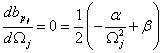(druhá rovnice)

· znají se frekvence a tlumení u dvou tvarů

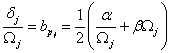(dvě rovnice)

· znají se frekvence a tlumení u více tvarů

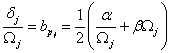(přeurčená soustava rovnic)

Kaskádový diagram

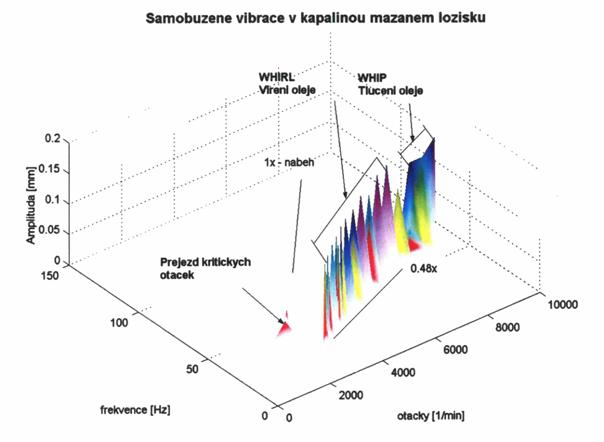
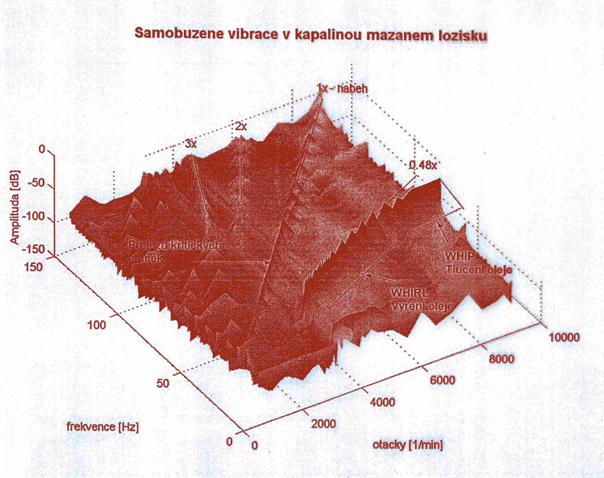
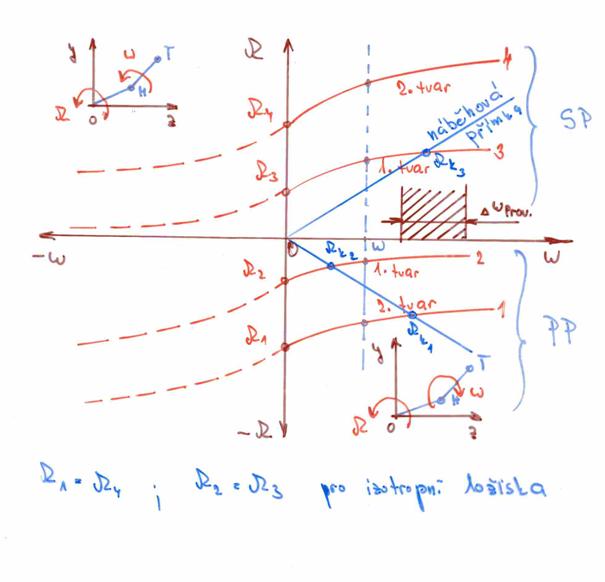
Stabilita pohybu

Stabilitu lze definovat z různých hledisek

· dynamická stabilita

· globální stabilita

· lokální stabilita

· stabilita struktury

· stabilita tvaru

· stabilita ve smyslu Lagrange

· stabilita ve velkém

· stabilita ve smyslu Ljapunova

· technická stabilita

Kritéria posouzení stability

· Na základě reálné části komplexní ho vlastního čísla

· Routhovo – Hurwitzovo kritérium

· Analýza ve fázové rovině

· Ljapunovy exponenty

· Floquetovo kritérium

· Analýza v Gausové rovině

Vlastní číslo - (stabilita typu divergence, nebo flutter)

Routhovo - Hurwitzovo kritérium

Ve staticky rovnovážné poloze je rychlost pohybu nulová. Jestliže na soustavu nepůsobí vnější síly, které nemají potenciál, staticky rovnovážná poloha se stanoví (na základě Lagrangeových rovnic II. druhu) z rovnice

Jednou z možností o rozhodnutí stabilní, či nestabilní rovnovážné polohy je druhá derivace, tedy pro stabilní rovnovážnou polohu misí být

O tom zda bude staticky rovnovážná poloha stabilní, nebo labilní lze rozhodnout např. na základě Routhova – Hurwitzova kritéria. Nejdříve je nutno sestavit tzv. charakteristickou rovnici

Nutnou a postačující podmínkou pro to, aby charakteristická rovnice měla všechny kořeny se zápornou reálnou částí je splnění nerovností:

2. , ,

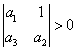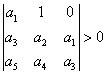Ljapunova definice stability v tzv. „malém“

Nerozrušený pohyb je stabilní, jestliže pro každé kladné malé číslo lze nalézt takové kladné číslo , že pro všechny rušivé pohyby pro které platí bude pro všechna . Jestliže takové neexistuje, pohyb je nestabilní.

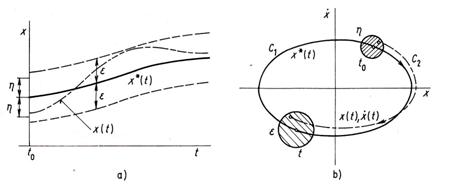
Fázová rovina (Hayashiho)

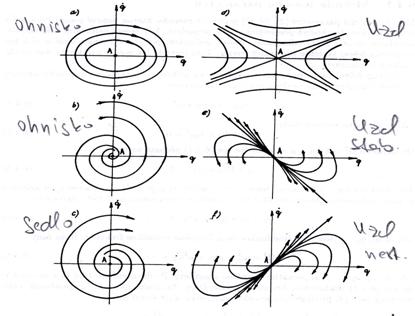
Jestliže se pohyb zastupujícího bodu blíží k ohnisku, dynamický systém je stabilní a pokud se vzdaluje, dynamický systém je nestabilní.

Ljapunovy exponenty

Exponenty polynomu rozhodují o stabilitě dynamického systému. Jejich výpočet je značně časově náročný a provádí se v časové oblasti.

Fluqetovo kritérium (Floquetova věta)

Floquetova teorie se vztahuje k soustavě lineárních obyčejných diferenciálních rovnic prvního řádu

kde matice A je spojitá periodická funkce s periodou T. Matice F se nazývá maticí fundamentálních řešení, přičemž sloupce jsou lineárně závislými řešeními. Pak lze řešení soustavy rovnic napsat ve tvaru

Matice

se nazývá přenosová, nebo také přechodová matice z času do času . Není-li matice funkcí času (konstantní), pak je matice přenosu dána vztahem

což je tzv. maticová exponenciála. Je-li matice funkcí času, pak je matice přenosu dána vztahem

Mezi časy 0 a T (perioda) pak je

nebo

(kdy je ). Matice se nazývá matice monodromie. Matice je dle Floquetovy věty regulární a rovnice představuje podobnostní transformaci (nemění se vlastní čísla matice před transformací a po ní). Pak vlastní čísla matice a matice jsou stejné. Pak stačí, posuzovat stabilitu pouze podle matice přenosu . Nutnou a postačující podmínkou pro to, aby dynamický systém byl stabilní je, aby velikost všech vlastních čísel mezi časy 0 a T ležela v rozsahu 0-1.

Stanovení matice (4 přístupy)

Homogenní tvar pohybových rovnic ve stavovém prostoru má tvar (pro zjednodušení zápisu je vynechán horní pruh)

tento lze upravit na tvar

nebo také

Matici přenosu je nejvýhodnější počítat numericky.

1. Přístup

Je-li časový úsek rozdělen na n časových kroků, pak

tedy přes maticovou exponenciálu

2. Přístup

Je-li časový úsek rozdělen na n časových kroků. Je-li časový krok integrace malý, lze během tohoto kroku považovat matici A za konstantní a platí

Při použití explicitní metody je

odtud

a matice přenosu mezi sousedními kroky výpočtu

3. Přístup

Je-li časový úsek rozdělen na n časových kroků. Je-li časový krok integrace malý, lze během tohoto kroku považovat matici A za konstantní a platí

Při použití implicitní metody je

odtud

a matice přenosu mezi sousedními kroky výpočtu

4. Přístup

Přímým výpočtem odezvy v čase T na základě zvolených počátečních podmínek. V podstatě se provádí opakovaně výpočet odezvy v čase T na základě zvolených počátečních podmínek. Tento výpočet se opakuje n krát.

K výpočtu odezvy v čase T lze využít některou z přímých metod integrace pohybových rovnic.

Poznámka: V případě použití metod přímé integrace pohybových rovnic lze rovněž využít Newmarkovu metodou, případně Runge – Kutha 4. řádu. Explicitní, nebo implicitní metoda zde byla ukázána pouze pro názornost

Analýza v Gausové rovině

Používá se při řešení vynuceného ustáleného kmitání. Pokud je pohyb zastupujícího bodu v Gausové rovině ve smyslu hodinových ručiček, dynamický systém je stabilní a naopak.

Poslední aktualizace

Menu