Dynamika rotorových soustav

6. Metody řešení dynamických vlastností rotorových soustav

frekvenčně modální vlastnosti

Problém vlastních hodnot

1. Standartní

2. Zobecněný

Standardní

Vychází se ze soustavy algebraických rovnic ve tvaru

Hledají se vlastní čísla matice , tak aby platilo

Příklad

Stanovte vlastní čísla matice

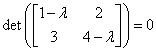
Po zpětném dosazení do soustavy algebraických rovnic nelze explicitně vypočítat , protože obě rovnice jsou lineárně závislé. Tedy např. pro první vlastní číslo

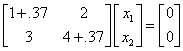
Obvykle se některá z neznámých volí a ostatní se dopočítávají.

Zobecněný

Vychází se z pohybové rovnice pro volné netlumené kmitání (volné kmitání)

Předpokládané řešení

a po dosazení

Zobecnění je dáno tím, že místo jednotkové matice je matice hmotnosti. Převedení na standardní se provede vynásobením

Nutnou a postačující podmínkou pro to, aby soustava rovnic měla nenulové netriviální řešení je, aby determinant matice soustavy byl roven nule.

Determinant se nazývá frekvenční determinant. Vlastní hodnoty jsou pro úlohy dynamiky vlastní frekvence kmitání dynamického systému (frekvenční spektrum). Neznámé v tomto případě představují pravostranné vlastní vektory (kmitna). Po uspořádání se obdrží modální matice pravostranných vektorů - . Obdobně bychom mohli stanovit levostranné vektory.

Levostranné vektory -

Po transponování této rovnice

Odkud se stanoví levostranné vlastní vektory. Vlastní čísla jsou stejné. V případě, že platí jsou levostranné a pravostranné vektory stejné

Normování

· Vzhledem k jedničce

· Vzhledem k matici hmotnosti

kde je spektrální matice

Podmínky ortogonality

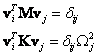
Podmínky ortoganility (kolmosti) vyjadřují nezávislost vlastních tvarů na sobě. Tato skutečnost má dva důsledky:

1. Při harmonickém buzení frekvencí rovné vlastní kmitá soustava pouze jediným tvarem kmitu s frekvencí rovnou budící frekvenci.

2. V případě, že je znám určitý tvar kmitání, nelze na základě této znalosti usuzovat jak budou vypadat (případně je odvodit) ostatní tvary kmitání.

Stavový prostor

V podstatě je to snížení řádu pohybové rovnice

Maticový zápis

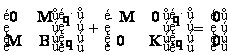
Zkráceně (pro volné kmitání v homogenním tvaru)

Horní podtržítka značí tzv. rozšířené veličiny. Předpokládané řešení

. reálná část komplexní ho vlastního čísla představuje tlumení a imaginární část vlastní frekvenci tlumeného kmitání.

Metody stanovení vlastních čísel a vektorů

· Frekvenční determinant

· Lancoszova metoda

· Metody založené na podobnostní transformaci

Metoda	Typ matice	Poznámka
Jacobi	symetrická	úplný problém
LR algoritmus	nesymetrická	úplný problém
QR algoritmus	nesymetrická	úplný problém
QZ algoritmus	nesymetrická	úplný problém
Lanczosova	nesymetrická	částečný
Mocninová	nesymetrická	částečný
Housenholderova	nesymetrická	částečný

Důležité veličiny

- vlastní číslo je komplexně sdružené

- vlastní frekvence netlumeného kmitání

- vlastní frekvence tlumeného kmitání

- součinitel doznívání, b – součinitel tlumení

kritický útlum -

- poměrný útlum

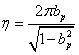- logaritmický dekrement útlumu

Stanovení tlumení z amplitudové charakteristiky. Šířka je stanovena pro amplitudu nebo při poklesu o 3 dB

Q - faktor

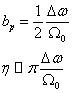
Pokles o 3 dB odpovídá hodnotě 70.7 %, nebo také hodnotě (nominální šířka pásma).

Vlastní hodnoty jsou obecně komplexně sdružená čísla. Reálná část odpovídá tlumení a imaginární je vlastní frekvence kmitání. Reálná část rozhoduje o stabilitě dynamického systému. Kladná znamená nestabilní a záporná stabilní. Vlastní čísla lze zobrazit v Gausově rovině. Každému vlastnímu číslu odpovídá i určitý tvar odezvy v časové oblasti.

Nelineární úlohy

Jak je známo, v nelineárních úlohách jsou obecně vlastní čísla závislá na amplitudách kmitání, rychlosti případně i na zrychlení. Výpočet vlastních čísel pak u nelineárních úloh rotorových soustav ztrácí smysl. V určitých případech za předpokladu kmitání soustav s malými výchylkami kolem rovnovážné soustavy lze řešit problém vlastních hodnot linearizované úlohy (např. za předpokladu trajektorie středu hřídele blízké kruhové trajektorii).

a) Mulerova metoda

Předpokládejme, že známe pro tři hodnoty frekvencí (pro začátek řešení stačí uvažovat nulovou reálnou část) tři hodnoty komplexního determinantu matice G, tedy

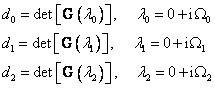
s následným výpočtem

a dále

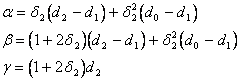
V dalším iteračním kroku se vypočítá

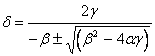
kde znaménko u druhé odmocniny se volí tak, aby se z obou možných hodnot jmenovatele určila v absolutní hodnotě větší. Nová hodnota komplexní frekvence se vypočítá dle vztahu

I když je začátek řešení pouze pro imaginární hodnoty frekvencí, procedura je naprogramována v komplexním oboru a celé řešení je od čtvrtého kroku prováděno v komplexním oboru. Iterační cyklus končí, je-li přírůstek absolutní hodnoty komplexní frekvence menší než zvolená přesnost řešení. Aplikace této metody vyžaduje alespoň přibližnou znalost vlastního čísla.

b) Metoda nalezení nulových bodů komplexní funkce

V tomto případě není znám exaktní tvar komplexní funkce, nýbrž jsou dány diskrétní hodnoty komplexního determinantu jako funkční hodnoty komplexní frekvence.

Podstatou algoritmu je nejdříve výpočet hodnot determinantu nad vymezenou oblastí (vhodná oblast je např. obdélník). Tato oblast je vymezena v Gausově rovině reálnými a imaginárními frekvencemi. V rovině jsou následně určeny isolinie jako spojnice bodů s nulovými reálnými, nebo imaginárními hodnotami komplexního determinantu. Ilustrativně jsou na obr. nakresleny spojnice nulových hodnot reálné a imaginární části komplexního determinantu. Z dvojice protínajících se křivek vždy jedna přísluší nulové reálné části a druhá nulové imaginární části komplexního determinantu. Na vodorovné ose jsou reálné a na svislé imaginární části komplexní frekvence, které se během výpočtu mění. Průsečík křivek s oběma nulovými hodnotami determinantu určují vlastní číslo soustavy. Z obr. 1.5.1 je zřejmých 5 vlastních čísel, z nichž dvě přísluší nestabilnímu dynamickému systému a zbývající stabilnímu. Dosavadní zkušenosti s aplikací této metody vykazují značnou numerickou stabilitu i pro případ značně přetlumených soustav.

l_Im

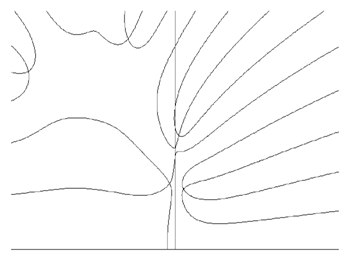-l_Re+l_Re

Obr. Spojnice nulových hodnot determinantu

Poslední aktualizace

Menu