Dynamika rotorových soustav

7. Metody řešení dynamických vlastností rotorových soustav

Přehled metod

1. Klasické řešení

2. Metoda trigonometrických kolokací

1. Klasické řešení

Vzhledem k předpokládanému řešení, do kterého může být obecně zahrnuta libovolná frekvence, případně násobek otáčkové frekvence je pro algoritmické zpracování na počítači vhodný tvar pohybové rovnice s nelineární funkcí na levé straně. Dále se předpokládá, že rotor kmitá malými výchylkami kolem rovnovážné polohy, která je např. u kluzného ložiska dána statickým zatížením. Při dalším zatížení vlivem nevývahy je trajektorie středu hřídele pro neisotropní ložiska eliptická kolem této rovnovážné polohy.

Při řešení soustavy nelineárních rovnic pro MKP i MDP byl sestaven algoritmus pro Aitkenovu a Newtonovu - Raphsonovu metou.

a) Aitkenova metoda v kombinaci s MKP

Při použití metody řešení nelineárních rovnic prostou iterací je nutno použít iterace s proměnným krokem, avšak je-li parciální derivace rovna 1 je iterační proces značně pomalý. Pro zrychlení konvergence lze použít např. Aitkenovu metodu, jejíž algoritmus je zde uveden. Protože se jednotlivé aproximace nepočítají pomocí jedné a téže funkce, jedná se tedy o nestacionární iterační proces.

Výchozí nelineární pohybová rovnice sestavená na bázi MKP má za předpokladu otáčkově závislého buzení tvar

(1)

Za předpokladu harmonického kmitání s frekvencí lze rovnici (1.5) po dosazení předpokládaného řešení obecně napsat ve tvaru

(1.6)

kterou lze zkráceně pro daný krok výpočtu zapsat v implicitním tvaru

(1.7)

K řešení této soustavy nelineárních rovnic je nutno použít iterační cyklus. Obecně lze použít cykly s pevným, nebo proměnným krokem. V nejjednodušším případě při aplikaci výše uvedené metody jde o metodu tříkrokovou. Posloupnost výpočtových kroků je pak následující

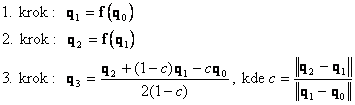(1.8)

Použitím této metody se současně zrychlí i iterační cyklus a tím i výpočet, proto se někdy v literatuře tento přístup neoznačuje jako metoda, ale pouze zrychlení iteračního procesu.

Pro dosažení požadované přesnosti lze použít několik přístupů. Doposud se nejlépe osvědčil přístup, kdy norma přírůstku deformace je menší, než určitá procentuální hodnota normy výchylky v kroku 3.

Výpočet se provádí pro reálnou a imaginární složku, resp. pro sin-ovou a cos-inovou složku odezvy pro oba směry kmitání. Tomu pak odpovídají i dvě složky rychlosti a zrychlení. Pro výpočet sil v ložisku (případně prvků v maticích) se použije pro tuhost reálná část výchylky, pro výpočet rychlosti imaginární část a pro zrychlení reálná.

b) Aitkenova metoda v kombinaci s MDP

Výchozí rovnice pro řešení v kroku na začátku iteračního cyklu má tvar

(1.9)

Algoritmus řešení je dále stejný jako pro kombinaci s MKP, který byl uveden výše. Rozdíl je ve třetím kroku, kde je nutno zvlášť provést výpočet pro část vektoru obsahujícího neznámé typu deformace a zvlášť pro část vektoru obsahujícího síly ve vazbách, včetně norem. Obdobným způsobem je nutno modifikovat výpočet v kritériu pro ukončení iteračního cyklu.

Algoritmus celkového řešení se skládá z těchto kroků

· Řešení problému vlastních hodnot „volného“ rotoru, na základě kterého se sestavuje matice „poddajnosti“ G^R.

· Řešení problému vlastních hodnot „volného“ statoru, na základě kterého se sestavuje matice „poddajnosti“ G^S. Tuto lze rovněž sestavit na základě experimentálně stanovených modálních vlastností.

· Řešení odezvy při vynuceném ustáleném kmitání „volného“ rotoru, na základě kterého se sestavuje vektor .

· Řešení odezvy při vynuceném ustáleném kmitání „volného“ statoru, na základě kterého se sestavuje vektor .

· Sestavení matice soustavy a vektoru pravé strany. Následuje její řešení včetně iterace, přičemž se po každé iteraci vypočítávají nové rychlosti. Iterační cyklus končí, když rozdíl příslušných výchylek a vazbových sil mezi prvním a třetím krokem řešení je dostatečně malý.

c) Newtonova - Raphsonova metoda v kombinaci s MKP

Algoritmus řešení soustavy nelineárních rovnic je následující. Označme C matici dynamických tuhostí, která má v našem případě má tvar

(1.9)

Předpokládejme, že známe řešení z předchozího otáčkového kroku, které označíme indexem - 1. V každém kroku řešení jsou dva kroky, přičemž druhý může být iterační.

1. Krok - Výpočet vektoru výchylek q_j

(1.10)

2. Krok - Výpočet vektoru „nevyrovnaných“ vnitřních sil podle vztahu

(1.11)

Dále se vypočítá přírůstek deformace od nevyrovnaných sil

(1.12)

Nová výchylka v kroku „“ pak je

. (1.13)

d) Newtonova - Raphsonova metoda v kombinaci s MDP

Její algoritmus je následující. Označíme-li matici soustavy G (výsledná matice sestavená na základě MDP, obsahující kromě příslušných matic dynamických poddajností nulové a jednotkové matice), vektor neznámých veličin q (zahrnuje posuvy i síly) a pravou stranu rovnice Q, (odezva volných soustav) první krok výpočtu pro budící frekvenci v předchozím kroku je

(1.14)

V druhém kroku (ten již je součástí iteračního cyklu) se zjistí vektor „nevyrovnaných“ vnitřních sil (setrvačných, tlumících i elastických), který zahrnuje i nevyrovnané výchylky i síly podle vztahu

(1.15)

Dále se vypočítá přírůstek výchylky a vazbových sil od nevyrovnaných výchylek a sil

(1.16)

a nová výchylka a vazbové síly v kroku „“

. (1.17)

Celý iterační cyklus pokračuje, až vektor nevyrovnaných sil je ve vhodném měřítku dostatečně malý.

Poznámky k řešení vynuceného ustáleného kmitání

V tomto případě má metoda MDP ve srovnání s klasickou MKP následující rozdíly:

· Matice G není matice dynamických tuhostí, která je nutná pro výpočet deformací

· Vektor vnitřních sil nevyjadřuje vnitřní síly v soustavě.

· Pravá strana rovnice (1.14) má tvar, který vyplývá z aplikace metody dynamických poddajností, tedy obsahuje výchylky volných podsystémů.

· Všechny navržené algoritmy byly autorem softwarově zpracovány a otestovány. Z řady provedených výpočtů nelineárních úloh rotorových soustav se více osvědčila klasická Newton-Raphsonova metoda, ve srovnání s modifikovanou.

· Pravá strana rovnice (1.15) je sestavena za základě výchylek i rychlostí v daném kroku řešení. Pro některé případy nelineárních funkcí docházelo ke ztrátě numerické stability řešení. Např. pro případ kluzných ložisek s relativní polohou středu hřídele blízkou jedné. Zlepšení numerické stability řešení lze dosáhnout pouze změnou výchylek a rychlost nechat stejnou jako v předchozím kroku řešení, tedy

(1.18)

2. Metoda trigonometrické kolokace

Řešení odezvy při vynuceném ustáleném kmitání, které bylo naznačeno v kapitole 1.2.3 a 1.3.3, předpokládá buzení i odezvu rovnou celočíselnému násobku otáčkové frekvence. U nelineárních úloh je známo, že v odezvě při buzení jednou harmonickou složkou jsou buzeny subharmonické, ultraharmonické, nebo subultraharmonické složky frekvence buzení.

Jeden z možných algoritmů řešení úloh je uveden např. v [15], kde je nelineární funkce uvažovaná na pravé straně pohybové rovnice. V některých případech je vhodnější zahrnovat přídavné účinky vazebných elementů na levou straně pohybové rovnice. Je to zejména v případě, kdy jsou známy tenzory přídavných hmotností, tlumení nebo tuhostí. Zahrnutí nelineárních vazebných elementů na levou stranu pohybové rovnice je také výhodné pokud se použijí MDP, případně MM, tedy kdy je nutno stanovit matice dynamických poddajností, nebo modální matice nelineárních vazeb.

2.1 Metoda trigonometrické kolokace v kombinaci s MKP

Buzení soustavy lze vyjádřit buď v reálném, nebo komplexním oboru. V této kapitole bude celá analýza provedena v reálném oboru. Předpokládejme, že buzení je periodické se známými násobky budící frekvence, které lze zapsat jako prvky množiny s prvky ve tvaru

(2.1)

kde . Např. pro nejvyšší stejné číslo v čitateli i jmenovateli 4 je množina násobků

(2.2)

Budící sílu při zahrnutí statického zatížení tak lze obecně vyjádřit ve tvaru

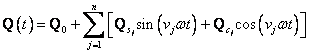(2.3)

kde indexy značí sinovou a kosinovou složku. Řešení pohybové rovnice předpokládejme ve stejném tvaru

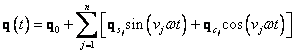(2.4)

Tuto metodu lze využít i při řešení nelineárních úloh. Pro obecnost předpokládejme, že i když vektor buzení bude obsahovat pouze jednu složku, řešení bude zahrnovat větší počet násobků budící frekvence. Volba počtu násobků v řešení závisí na typu nelineární úlohy.

Nelineární pohybová rovnice s ohledem na aplikaci metody trigonometrické kolokace v rotorových soustavách má tvar

(2.5)

Z rovnice (2.4) pro rychlost a zrychlení platí

(2.6)

Po dosazení (2.6), (2.3) a (2.4) do (2.5) a porovnáním členů u stejných neznámých se po úpravě obdrží

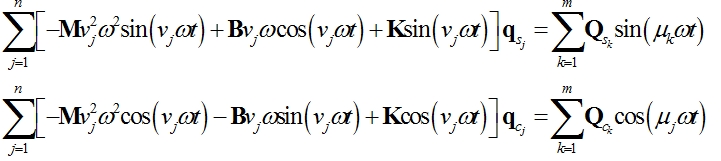
Označení pro kolokační čas

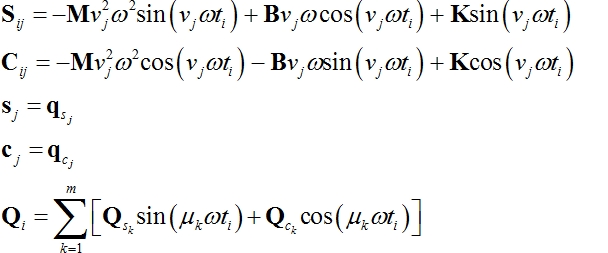
Zkráceně pak

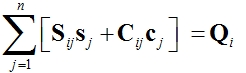
Goniometrické funkce v rovnicích jsou pro daný čas a násobek konstanty. Konkrétní časové okamžiky se stanoví rozdělením nejmenší periody v požadovaném spektru odezvy na konečný počet hodnot. Pak má pohybová rovnice má tvar

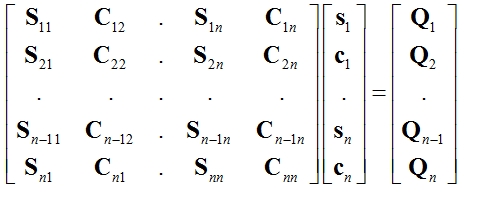
2.2 Metoda trigonometrické kolokace v kombinaci s MDP

S ohledem na aplikaci MDP bude v této kapitole provedena analýza v komplexním oboru. Uvažujme soustavu s jedním hřídelem. Dále předpokládejme, že „volná“ rotorová i statorová soustava jsou lineární a vazebné prvky mezi oběma částmi jsou nelineární. V dalším se zaměřme pouze na řešení ustálené složky odezvy při kmitání kolem známé rovnovážné polohy. Znamená to tedy, že např. pro kluzné ložisko je nalezení staticky rovnovážné polohy provedeno před analýzou vynuceného ustáleného kmitání.

Buzení i odezvu soustavy předpokládejme ve tvaru

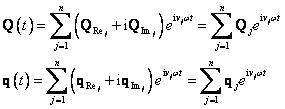(2.11)

Za předpokladu shodných pravostranných a levostranných vlastních vektorů statoru se dynamická poddajnost statoru pro tvarů kmitu a -tou složku budící frekvence vypočítá ze vztahu

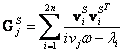(2.12)

Dynamická poddajnost samostatné „volné“ rotorové části odpovídající -té složce budící frekvence se stanoví na základě vztahu

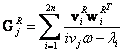(2.13)

kde „“ a „“ představují pravostranné a levostranné vlastní vektory.

Rozdělením dynamické poddajnosti „volného“ rotoru na submatice, jejichž řád je specifikací míst buzení a místy vazeb mezi rotorem a statorem pro -tou složku buzení je

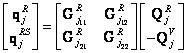(2.14)

Za předpokladu, že je řešen „volný“ rotor () pro -tou složku odezvy na rotoru a v místech vazeb se statorem plynou z rovnice (2.14) vztahy (dolní index „v“ značí že se jedná o „volnou“ soustavu)

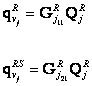(2.15)

nebo také

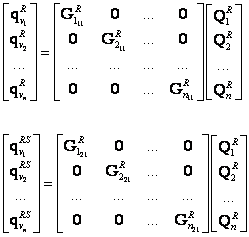(2.16)

a zkráceně

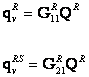(2.17)

Pro -tou složku „samostatné“ statorové část platí pro odezvu v místech vazeb s rotorovou částí vztah

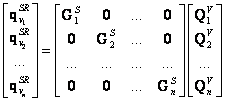(2.18)

a zkráceně

(2.19)

Odezvy samostatných částí lze řešit pouze pro příslušné -té složky buzení, protože vzhledem k lineárnímu systému jsou odezvy na ostatních násobcích nulové.

Vzhledem k tomu, že poddajnosti rotorové a statorové části jsou vyjádřeny v komplexním oboru, je nutno i vazby analyzovat v komplexním oboru. Pro vazebné členy mezi rotorem a statorem, které mohou tvořit samostatný dynamický subsystém, lze při použití podmínek rovnováhy a kompatibility pohybovou rovnici psát ve tvaru

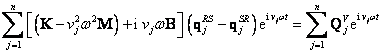(2.20)

kde matice jsou obecně nelineární funkční závislosti na výchylce a rychlosti a jejich řád je v případě uvažování pouze posuvů dvojnásobný počtu vazeb mezi rotorem a statorem. Zkráceně lze tuto rovni pro -tý kolokační čas vyjádřit jako

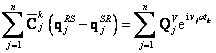(2.21)

kde

(2.22)

Rovnice (2.21) po detailnějším zápisu pro kolokačních časů je

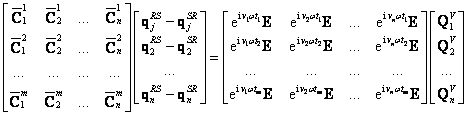(2.23)

kde je jednotková matice, jejíž řád při uvažování pouze posuvů je roven dvojnásobnému počtu vazeb. Stejný řád mají i příslušné submatice. Rovnici (2.23) lze zapsat ve tvaru,

(2.24)

přičemž horní index značí, že se matice týkají vazeb. Obecně obdélníková matice na pravé straně této rovnice obsahuje pro konkrétní kolokační časy čísla. Po úpravě má tvar

(2.25)

nebo také

(2.26)

kde

(2.27)

Výsledná rovnice pro řešení vynuceného ustáleného kmitání má na základě rovnic (2.14), (2.17), (2.19) a (2.26) po úpravě tvar

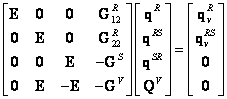(2.28)

Jestliže označíme počet míst na rotoru se specifikovaným buzením, nebo také místa s požadovanou odezvou (při nulovém buzení), počet míst s vazbami mezi rotující a nerotující částí, a dále počet požadovaných násobků budící frekvence v odezvě, pak jednotlivé matice jsou:

- blokově diagonální matice řádu , která se obdrží z výsledné matice

sestavené s lokálních na základě rovnice (2.14).

- blokově diagonální matice řádu , která se obdrží z výsledné matice

sestavené s lokálních na základě rovnice (2.14).

- blokově diagonální matice řádu na základě rovnice (2.18).

- plná matice řádu na základě rovnic (2.23), (2.24) a (2.27).

Zkráceně lze (2.28) zapsat ve tvaru

(2.29)

což je soustava obecně nelineárních rovnic algebraických rovnic. K jejímu řešení lze použít některý z algoritmů uvedených v dalších kapitolách.

Tvar rovnice (2.28) je po formální stránce shodný s tvarem pro řešení odezvy při uvažování buzení i odezvy s jednou harmonickou složkou (viz. rov. (1.2.18)). V případě uvažování buzení s více složkami jsou matice dynamických poddajností rotorové a statorové části blokově diagonální, matice dynamických poddajností vazebných elementů je plná.

Obdobným způsobem lze řešit i odezvu soustavy se dvěma koaxiálními hřídeli. Výsledná rovnice pro řešení odezvy při uvažování pouze jedné frekvenční složky buzení i odezvy má na základě rovnice (1.3.36) tvar

(2.30)

Při uvažování více složek buzení jsou matice příslušející rotorům a statoru blokově diagonální a matice dynamických poddajností příslušející vazbám plné v obecném případě s nelineárními prvky. Řád jednotkových a nulových matic je stejně jako v předchozím případě závislý na počtu specifikovaných míst s požadovaným buzením a odezvou na rotorech a počtu vazeb mezi rotory a se statorem.

Poznámka 1

Řešení odezvy dle rovnice (2.10) je prováděno v reálném oboru, zatímco rovnice (2.28) a (2.30) jsou v oboru komplexním. Jak již bylo uvedeno, výhodou této metody je,že umožňuje uvažovat funkční závislosti nelineárních vazeb ve tvaru vhodném pro řešení odezvy při přechodovém kmitání, tedy v reálném oboru. V tomto případě se do funkčních závislostí dosazuje pro danou složku odezvy modul výchylky. Je tedy uvažován horní odhad výchylky. Znamená to, jakoby v daný časový okamžik byly maximální výchylky všech násobků ve fázi.

Poznámka 2

Celkový algoritmus řešení odezvy při vynuceném ustáleném kmitání metodou trigonometrické kolokace ať u soustav s jedním hřídelem, nebo s koaxiálními je tedy následující:

· Výpočet modálních vlastností „volných“ rotorových soustav.

· Výpočet modálních vlastností „volné“ statorové soustavy, nebo jejich stanovení experimentálně.

· Výpočet odezvy „volných“ rotorových soustav. Vzhledem k předpokládaným lineárním soustavám, na základě principu superpozice lze výpočet provést opakovaně pro daný násobek budící frekvence.

· Sestavení matice soustavy a pravé strany pro řešení soustavy nelineárních rovnic, přičemž v každém kroku iterace a konkrétní kolokační čas je nutno sestavit výslednou odezvu a rychlost, na základě kterých se stanoví přídavné hmotnosti, tlumení a tuhost nelineárních vazeb.

Poslední aktualizace

Menu

Poznámky k řešení vynuceného ustáleného kmitání

Poznámka 1