 Dynamika rotorových soustav
Dynamika rotorových soustav
12. Dynamika volných a olopatkovaných disků
ÚVOD
Základem pro analýzu za rotace je znalost frekvenčně modálních vlastností za klidu. K tomu lze s výhodou využít vlastností rotačně periodických struktur (dále v textu RPS), což je paměťově i časově málo náročné. Pro analýzu vybuditelnosti tvarů kmitání za rotace, zejména olopatkovaných disků, je již nutný tzv. „plný“ model, tedy celé olopatkované kolo. Výpočet se provádí v časové oblasti a představuje výpočtovou simulaci chování disku za rotace. V takovém případě lze předpokládat ustálený provozní stav, případně analyzovat odezvu při zadané změně otáček. Již z tohoto je zřejmé, že tato výpočtová analýza značně závisí na dobré znalosti vstupních dat.
V textu bude provedena teoretická analýza dynamických vlastností disků, na modelové úloze ukázán princip analýzy a text bude doplněn analýzou reálného olopatkovaného kola.
DYNAMICKÉ VLASTNOSTI NEOLOPATKOVANÝCH DISKŮ
Disk jakožto kontinuum má nekonečný počet vlastních frekvencí a tvarů kmitání. Teoretický základ popisující dynamické vlastnosti za klidu je uveden např. v [1]. Základní tvary kmitání jsou charakterizovány uzlovými průměry a kružnicemi. Na obr. 1 jsou nakresleny tvary kmitání s uzlovými průměry, kružnicemi nebo jejich kombinací. V případě, že se provádí analýza s využitím MKP je vhodné provést výpočet i s vlivem odstředivých sil, které disk vyztužují. Výsledkem této analýzy je závislost vlastních frekvencí na uzlových průměrech.
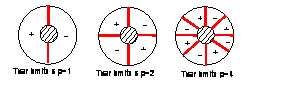
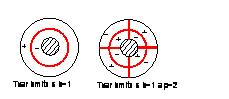
Obr. 1 Tvary kmitání disků
Při
experimentální analýze za rotace kdy je disk buzen, se po disku šíří dvě vlny,
které běží proti sobě. Vznikne stojaté vlnění. Za rotace se vlna, která se šíří
ve stejném smyslu jako je úhlová rychlost
rotace, nazývá dopředná (označeno +), a té která se šíří pro jejímu smyslu se
říká zpětná (označeno -). Z pohledu pozorovatele, který je v klidu,
jsou úhlové rychlosti obou vln pro ![]() -tý násobek úhlové
rychlosti otáčení dány vztahy
-tý násobek úhlové
rychlosti otáčení dány vztahy
![]() (1)
(1)
Z pohledu vybuditelnosti daného tvaru kmitání má největší význam tzv. „vlna stojící v prostoru, tedy kdy vlna běžící vzad má nulovou úhlovou rychlost. V takovém případě během otáčení jsou místa s uzly trvale v klidu. Otáčky při kterých dochází k výraznému vybuzení se nazývají kritické otáčky disků. Násobek otáčkové frekvence je shodný s počtem uzlových průměrů, tedy
![]() (2)
(2)
DYNAMICKÉ VLASTNOSTI OLOPATKOVANÝCH DISKŮ
Dynamické vlastnosti olopatkovaných disků jsou velmi podobné s dynamickými vlastnostmi neolopatkovaných disků. Podstatný vliv pouze má počet rotorových lopatek. V obecném případě, kdy je určitý počet lopatek spojen do jednoho celku, je olopatkovaný disk charakterizovaný určitým počtem struktur. V řadě případů, s ohledem na tuhostní a hmotnostní parametry se mohou vyskytnout uzlové kružnice procházející lopatkami, což v podstatě znamená, že lopatky kmitají některým z vyšších tvarů kmitů.
Také u
olopatkovaných disků dochází při určitých otáčkách k výraznému vybuzení
určitých tvarů kmitání. Tyto otáčky se
periodicky vzhledem k násobku, která je roven
počtu rotorových lopatek (struktur). Kompletní Campbellův diagram pro tvar
kmitu, který je dán ![]() uzlovými průměry je na obr. 2.
uzlovými průměry je na obr. 2.
DYNAMICKÉ VLASTNOSTI ROTAČNĚ PERIODICKÝCH STRUKTUR
Výpočtový model s využitím MKP lze sestavit pro celé kolo včetně lopatek, což se zpravidla označuje jako „plný“ model. Druhý přístup vychází z představy, že se jistá část disku a lopatek po obvodu kola periodicky opakuje. V takovém případě se jedná o tzv. „rotačně periodickou strukturu“. Výpočet dynamický vlastností pak lze provést na plném, nebo značně zjednodušeném modelu. Časová náročnost výpočtů na obou modelech je nesrovnatelná. Modální analýzu a odezvy při vynuceném ustáleném kmitání lze provést s využitím vlastností rotačně periodických struktur.
V dalším části bude na jednoduché úloze ukázán přístup s využitím obou modelů. Modelová úloha je tvořena diskrétními hmotnými elementy spojenými mezi sebou pružným a tlumícím členem. Soustava je připevněna k základnímu tělesu z důvodu eliminace nulových vlastních frekvencí.
Řešení jako celek – plný model
Schéma části
struktury je na obr. 3. Předpokládejme, že počet rotačně periodických struktur
je ![]() .
Dále, že soustava kmitá
.
Dále, že soustava kmitá ![]() uzlovými průměry. Pro úhel
připadající na jednu strukturu platí vztah
uzlovými průměry. Pro úhel
připadající na jednu strukturu platí vztah ![]() . Pro potenciální
energii pak platí
. Pro potenciální
energii pak platí
 (3)
(3)
kde ![]() . Obdobně pro zatlumenou
funkci
. Obdobně pro zatlumenou
funkci
![]() (4)
(4)
![]() (5)
(5)
Pohybová rovnice celé struktury má pak tvar
![]() (6)
(6)
Řešení na základě vlastností RPS
Úplně uvolněná jedna struktura je na obr. 4. Pro tuto strukturu lze psát pohybovou rovnici ve tvaru
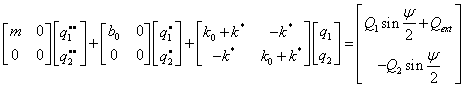 (7)
(7)
Fázové posunutí pohybujících se
uzlů je dáno vztahem ![]() . Pak pro deformační a silové
parametry v místech řezu platí
. Pak pro deformační a silové
parametry v místech řezu platí
![]() (8)
(8)
Mezi základní dynamické vlastnosti patří modální analýza, odezva při vynuceném ustáleném a přechodovém kmitání.
Modální analýza, tedy výpočet vlastních čísel a vlastních vektorů nepředpokládá vnější buzení. Pohybové rovnice pak mají tvar
 (9)
(9)
Pro předpokládané harmonické kmitání lze psát
![]() (10)
(10)
Pak po dosazení
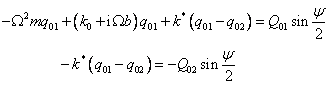 (11)
(11)
kde dále v druhé rovnici po úpravě je
![]() (12)
(12)
a po dosazení do první rovnice
![]() (13)
(13)
a další úpravou
![]() (14)
(14)
a dále
![]() (15)
(15)
odkud pro tlumenou soustavu¨
![]() (16)
(16)
odkud pro netlumenou soustavu
![]() (17)
(17)
Poslední dvě rovnice v obecném případě představují tzv. frekvenční determinant, na základě kterého se hledají jeho nulové body.
Odezva při vynuceném ustáleném kmitání
Vlastnosti rotačně periodických struktur lze využít i při řešení odezvy při vynuceném ustáleném kmitání. Pohybová rovnice má tvar
![]() (18)
(18)
odkud
![]() (19)
(19)
MODELOVÁ ÚLOHA
Jako modelová úloha byla zvolena soustava s hodnotami diskrétních parametrů
|
Označení |
|
|
|
m |
r |
s |
|
Hodnota |
1000 N/m |
0 Ns/m |
1.E6 N/m |
1 kg |
8 |
22 |
Tabulka I Vstupní parametry modelové úlohy
Cílem analýzy je stanovení modálních vlastností za rotace a zejména analýza vybuditelnosti tvaru kmitu se dvěma uzlovými průměry při různých otáčkách.
Modální vlastnosti za klidu a za rotace
Analýza modálních vlastností byla provedena s využitím výše uvedeného matematického modelu, přičemž výpočtový model byl sestaven v jazyce MATLAB. S ohledem na model lze analyzovat pouze tvary kmitu charakterizované uzlovými průměry. Dále s ohledem na počet rotorových lopatek, lze analyzovat tvary kmitu maximálně se 4 uzlovými průměry. Na obr. 5 je nakreslena závislost vlastních frekvencí na uzlových průměrech
Následně je na obrázku 6 je nakreslen Campbellův diagram zejména s ohledem na analýzu vybuditelnosti tvaru kmitu se 2 uzlovými průměry. Detail tohoto diagramu s ohledem na násobek 22, který je roven počtu statorových lopatek na obr. 7.
Na obrázcích 6 a 7 jsou kroužky vyznačeny body (zejména následně otáčky), při kterých nastává výrazné vybuzení tvaru kmitu s určitým počtem uzlových průměrů. Při další analýze bude zaměřena pozornost zejména na buzení 22 statorovými lopatkami a na tvar kmitu se dvěma uzlovými průměry s frekvencí 86,3 Hz. V tabulce II jsou uvedeny kritické otáčky odpovídající vybuzení tohoto tvaru kmitu při různých násobcích
|
Násobek |
k=2*r-p |
k=r+p |
k=r-p |
k=p |
|
Násobek |
14 |
10 |
6 |
2 |
|
Kritické otáčky [1/min] |
370 |
518 |
863 |
2588 |
Tabulka II Kritické otáčky olopatkovaného disku
Poznámka
V technické praxi je poměrně častý případ, kdy jsou lopatky kol svázány vazebnými elementy. V poslední době se výhradně používají tzv. „tlumící“ elementy, které nejsou pevně spojeny s lopatkami, přičemž k vazbě dochází v důsledku odstředivých sil. Vazebný element se v jejím důsledku přitlačí k lopatce a na základě velikosti odstředivé a třecí síly dochází ke kontaktu. Modelování kontaktu s vlivem pasivních odporů patří v současné době k nejobtížnějším a nejvíce diskutovaným fenoménem v dynamice olopatkovaných sil. Jako poznámka k této problematice jsou na obr. 12 a 13 prezentovány Campbellovy diagramy olopatkovaného kola, přičemž v jednom případě je vazebný element tlumící drát a ve druhém případě je drát pájený k lopatkám. Ve druhém případě tedy nedochází ke vzájemnému prokluzu mezi lopatkou a drátem. Již z vizuálního porovnání je zřejmý podstatný rozdíl. V případě pájeného drátu je zcela evidentní, že kolo v celém analyzovaném pásmu otáček má tzv. svazkový charakter. V případě tlumícího drátu je zřejmé, že dochází ke vzájemnému prokluzu mezi lopatkou a drátem, ale třecí síly mají za následek, že celá soustava má již charakter svazkového kmitání s určitým počtem uzlových průměrů. To je velmi důležitý závěr (podrobnosti viz [5]).
TECHICKÁ APLIKACE
Geometrie modelu vychází z modelu segmentu s trojicí lopatek. Vzhledem k tomu, že posouzení vybuditelnosti příslušných tvarů kmitání za rotace lze provést jedině na plném modelu, bylo potřeba model upravit a vzhledem k možnostem dostupné výpočetní techniky i zjednodušit. Původní model měl detailně vymodelován vidličkový závěs a byl vytvořen jako sestava. Byl respektován kontakt mezi jednotlivými částmi, což vedlo na nelineární úlohu. Proto byly kontaktní prvky nahrazeny pevnou vazbou.
Disk je vyroben z oceli. Bylo předpokládáno, že nedojde k překročení
oblasti ve které se materiál chová lineárně pružně. Byl tedy zvolen materiál
lineární izotropní. Modul pružnosti ![]() byl zvolen
byl zvolen ![]() a
Poissnovo číslo
a
Poissnovo číslo ![]() , což jsou pro ocel běžně užívané
hodnoty. Úlohy, ve kterých se při řešení objevuje i matice
hmotnosti vyžadují zadání hustoty materiálu. Pokud se
rozměry budou zadávat v milimetrech, modul pružnosti v megapascalech, musí být
hustota zadána v tunách na milimetr krychlový. Tedy
, což jsou pro ocel běžně užívané
hodnoty. Úlohy, ve kterých se při řešení objevuje i matice
hmotnosti vyžadují zadání hustoty materiálu. Pokud se
rozměry budou zadávat v milimetrech, modul pružnosti v megapascalech, musí být
hustota zadána v tunách na milimetr krychlový. Tedy ![]() .
.
Pro analýzu dynamických vlastností je vhodná hrubá pravidelná síť. Bylo zkoušeno několik variant sítí s různou hustotou a různými prvky, aby bylo dosaženo co nejmenšího počtu stupňů volnosti, tedy i co nejkratších výpočtových časů a zároveň aby se výsledky modální analýzy příliš nevzdalovaly výsledkům získaných modální analýzou výše zmíněného segmentu trojice. Nakonec byly použita síť generována strukturními prvky SOLID 45 s lineární bází. Tento model měl 32000 uzlů.
Modální analýza byla řešena v programu ANSYS metodou block Lanczos. Frekvenční rozsah byl zvolen od 0 Hz do 2500 Hz. Výpočty ukázaly, že zpevnění odstředivými silami nemá podstatný vliv na vlastní frekvence.
Okrajové podmínky v tomto případě představují uchycení disku na hřídeli. Kmitání hřídele bylo považováno za nepodstatné. Do uzlů na vnitřní ploše disku byly předepsány nulové posuvy jak ve směru axiálním, tak i ve směru radiálním a tečném.
Porovnání vlastních frekvencí tohoto modelu s vlastními frekvencemi původního segmentu s trojicí lopatek ukázalo, že vlastní frekvence se rozchází pouze u vlastních tvarů s malým počtem uzlových průměrů. S rostoucím počtem uzlových průměrů se k sobě přibližují. U vlastního tvaru se čtyřmi uzlovými průměry je rozdíl mezi vlastními frekvencemi obou modelů 6%. Ovšem došlo v výraznému zkrácení času potřebného k vyřešení. Na obr. 15 je znázorněna závislost počtu uzlových průměrů na frekvenci. Červeně je vyznačen stav, který bylo rozhodnuto budit. Je na něm vyznačeno i omezení rozsahu frekvencí při modální redukci.
Při výpočtu odezvy při nestacionárním kmitání
byl olopatkovaný disk je buzen tlakovým úplavem za statorovou mříží. V reálné
turbíně je statorová mříž v klidu, a disk rotuje. Během rotace procházejí
lopatky rotoru tlakovými úplavy, čímž dochází k buzení. Při řešení této úlohy
je výhodnější použit přístup, ve kterém se předpokládá, že disk stojí a rotuje
tlakové pole. Z tlakového pole se stanoví síly,
které pak lze předepsat jako časově proměnné zatížení na každé lopatce. Je
potřeba rozhodnout které otáčkové režimy se budou dále analyzovat a podle toho
stanovit frekvenci budících sil. V tomto případě bylo rozhodnuto zaměřit
se na vybuzení stavu, při kterém disk kmitá tvarem
se čtyřmi uzlovými průměry, tedy ![]() . Tomuto stavu odpovídá
vlastní frekvence určená modální analýzou
. Tomuto stavu odpovídá
vlastní frekvence určená modální analýzou ![]() . Kritické
otáčky lze stanovit z Campellova diagramu jak je naznačeno na obr. 2. Disk
má 54 lopatek, z nichž každé tři jsou nahoře spojeny bandáží, takže tvoří
18 struktur (
. Kritické
otáčky lze stanovit z Campellova diagramu jak je naznačeno na obr. 2. Disk
má 54 lopatek, z nichž každé tři jsou nahoře spojeny bandáží, takže tvoří
18 struktur (![]() ).
Hodnoty kritických otáček pro různé násobky jsou uvedeny v tabulce III.
).
Hodnoty kritických otáček pro různé násobky jsou uvedeny v tabulce III.
|
Násobek |
k=2*r-p |
k=r+p |
k=r-p |
k=p |
|
Násobek |
32 |
22 |
14 |
4 |
|
Kritické otáčky [1/min] |
3262,5 |
4745,5 |
7457 |
26100 |
Tabulka III Kritické otáčky
Při stanovení buzení výpočtová analýza v CFD ukázala, že časový průběh buzení lze poměrně dobře aproximovat harmonickým průběhem. Obecná síla byla rozložena na axiální a tangenciální složku a na jednotlivé lopatky byly předepsány síly pomocí funkce
![]() ,
, ![]() (22)
(22)
kde ![]() , resp.
, resp. ![]() je amplituda axiální,
resp. tangenciální složky síly,
je amplituda axiální,
resp. tangenciální složky síly, ![]() je úhlová
frekvence buzení,
je úhlová
frekvence buzení, ![]() je fázový posun a
je fázový posun a ![]() je pořadí
rotorové lopatky.
je pořadí
rotorové lopatky.
K integraci pohybové rovnice byla požita implicitní Newmarkova metoda. Tato metoda je nepodmíněně stabilní. Přesnost řešení závisí na délce integračního kroku, který by měl být kratší, než desetina nejkratší periody. Příliš hrubé dělení vede ke zkresleným výsledkům, naopak příliš jemné dělení zbytečně prodlužuje čas simulace. Celkový čas byl zvolen tak, aby se disk během simulace otočil desetkrát. Konkrétní délky integračních kroků jsou v tabulce IV.
|
Násobek |
32 |
22 |
14 |
4 |
|
Integrační krok [s] |
1,84e-1 |
1,26e-1 |
8,05e-2 |
2,30e-2 |
Tabulka IV Integrační krok
Proporcionální tlumení je definováno
koeficienty ![]() a
a
![]() . Je
vyjádřeno vztahem
. Je
vyjádřeno vztahem
![]() (23)
(23)
![]() je matice tlumení, člen
je matice tlumení, člen ![]() přestavuje
vnější konstrukční tlumení a člen
přestavuje
vnější konstrukční tlumení a člen ![]() nahrazuje vnitřní materiálové
tlumení. Pro výpočtovou analýzu byly zvoleny hodnoty
nahrazuje vnitřní materiálové
tlumení. Pro výpočtovou analýzu byly zvoleny hodnoty ![]() a
a ![]() .
.
Metoda použitá
k řešení přechodového kmitání je
v ANSYSu označena jako „Mode Superposition Method“, což je metoda, která
pracuje s modální redukcí a při řešení vyžaduje soubor dat z
modální analýzy. Výsledkem analýz přechodového
kmitání byly soubory dat, ve kterých byly zapsány
posuvy všech uzlů ve všech třech směrech a ve všech časových krocích. K následnému
zpracování nebylo třeba tolik hodnot. Bylo rozhodnuto dále zpracovávat pouze
posuvy ve směru osy disku (osa rotoru z ) a pouze ve vybraných uzlech.
Zvoleny byly uzly ležící na vnějším obvodu bandáže na hraně tlumícího pásku.
Hodnoty výše zmíněných posuvů v těchto uzlech byly vypsány do samostatného
textového souboru, který byl dále zpracováván v programu MATLAB. Na tyto
data byl aplikován algoritmus FFT. Ve Fourierově spektru se kromě očekávané
frekvence buzení a vlastní frekvence objevila ještě jedna nižší frekvence.
Pravděpodobně došlo k vybuzení vlastní frekvence
lopatky. Aby nedošlo k vybuzení této frekvence,
lze využít vlastnosti modální redukce, která umožňuje zahrnout do řešení pouze
určitý počet vlastních tvarů. Vzhledem
k použité metodě řešení toho lze dosáhnout omezením rozsahu frekvencí u
modální analýzy. V tomto případě byl nový rozsah frekvencí zvolen od
1000 Hz do 2000 Hz. Ve Fourierově spektru se zobrazí pouze
vlastní frekvence a frekvence buzení. Odezva
olopatkovaného disku při násobku budící frekvence ![]() je na obr. 14.
je na obr. 14.
ZÁVĚRY
Základem pro komplexní analýzu dynamických vlastností olopatkovaných kol a disků je frekvenčně modální analýza, a také výpočtová simulace chování lopatkové řady za rotace. Frekvenčně modální analýza nedává představu o vybuditelnosti jednotlivých tvarů kmitání. Teprve analýza odezvy při přechodovém kmitání, což je výpočtová simulace dynamického chování při daných provozních podmínkách dává představu o reálném chování. Protože se simuluje dynamické chování při daných provozních podmínkách, je velmi důležité mít k dispozici správný výpočtový model, zejména tlumící vlastnosti a provozní buzení. Výpočtová simulace na modelové úloze i na reálném kole ukázala, že při různých provozních stavech může nastat kmitání, kdy určitá část olopatkovaného disku kmitá výrazněji, než ostatní části. Počet těchto míst je po obvodu periodicky rozmístěn a má charakter velmi podobný stojatému vlnění, kdy vlna běžící vzad má nulovou úlovou rychlost.
LITERATURA
[1] Juliš, K., Brepta, R., a kol.: Mechanika II. díl – dynamika. SNTL Praha 1987.
[2] Chronin, A., V.: Kolebanie diskov. Moskva 1970.
[3] Hamid, M.: Forced vibration of rotating disc and interaction with nonrotaring structures, Imperial College of Science, Technology and Medicine, London, 1991.
[4] Doležal, Z.: Základní rozbor provozního buzení a kmitání oběžných kol radiálních kompresorů. VZLÚ Praha, V-1446/82, Praha 1982.
[5] Malenovský,
E.: Teoreticko experimentální analýza dynamiky lopatkování koncových stupňů
parních rychloběžných turbin. kandidátská disertační práce, VUT FSI Brno, Brno
1985, 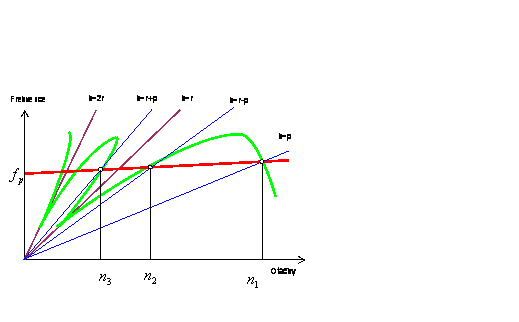

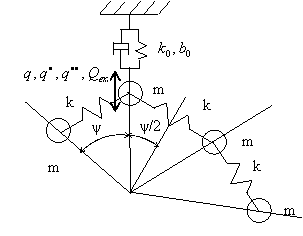

Obr. 2 Campbellův diagram olopatkovaného disku Obr. 3 Schéma jedné části struktury
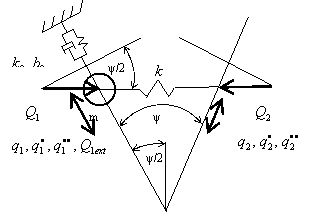

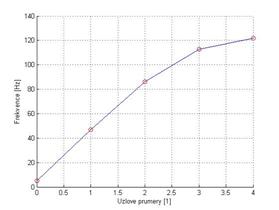
Obr. 4 Částečně uvolněná jedna struktura Obrázek 5 Závislost frekvence na uzlových průměrech.
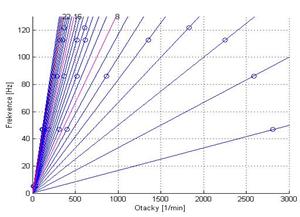
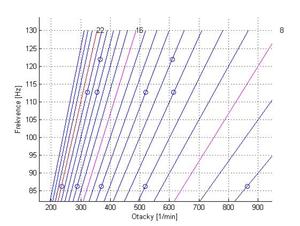
Obr. 6 Campbellův diagram Obr. 7 Detail Campbellova diagramu
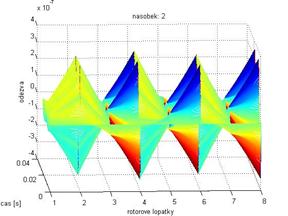
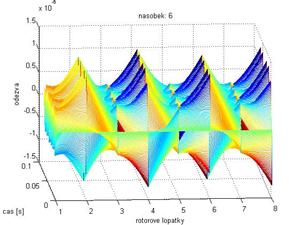
Obr. 8 Odezva při násobku 2 Obr. 9 Odezva při násobku 6
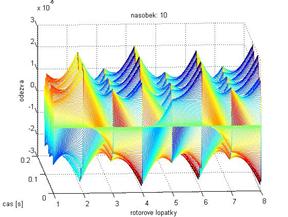
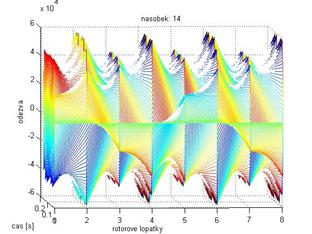
Obr. 10 Odezva při násobku 10 Obr. 11 Odezva při násobku 14
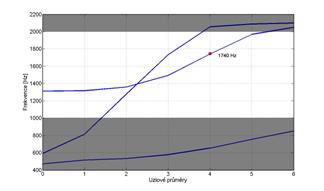
Obr. 14 Závislost frekvencí na uzlových průměrech
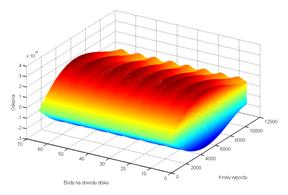
Obr. 15 Odezva při násobku 32