6. Redukce počtu stupňů volnosti

 

O životnosti a spolehlivosti soustav rozhodují do značné míry i její dynamické vlastnosti. Proto se soustavy, u nich se předpokládá dynamické zatěžovaní, již v návrhu podrobují dynamickým analýzám. Při odvozování matematických modelů se za účelem respektování co největší možné míry shody s geometrií reálného tělesa nebo soustavy a z důvodů zmenšení chyb způsobených aproximacemi volí velký počet stupňů volnosti. Počet stupňů volnosti může být až řádu 10⁶. Takto sestavené modely však neumožňují efektivní a rychlý způsob výpočtu dynamických vlastností. Proto se využívá možnosti, že pro zjišťování dynamických vlastností stačí využít jen omezené frekvenční pásmo, ve kterém předpokládáme buzené soustavy (ev. násobek tohoto pásma) a proto můžeme matematickým postupem snížit počet stupňů volnosti tělesa nebo soustavy, za předpokladu, že nedojde k výrazným změnám dynamických vlastností. Tento proces se nazývá redukce počtu stupňů volnosti nebo také někdy kondenzace.

Redukci počtu stupňů volnosti si tedy můžeme jednoduše definovat jako transformaci modelu z prostoru dimenze n do prostoru dimenze m, přičemž platí, že , a dojde k přibližnému zachování základních dynamických vlastností v jistém frekvenčním intervalu.

Rozsah redukce lze zadat podle následující formule: Požadujeme-li u redukovaného modelu vypočítat p prvních vlastních frekvencí blízkých vlastním frekvencím neredukovaného modelu, musí počet redukovaných stupňů volnosti n splňovat podmínku:

 

 

6.1 Redukce transformací zobecnělých souřadnic

 

Mějmetransformační matici, obecně typu . Transformaci souřadnic rozumíme potom předpis

            .

Provedeme-li tuto transformaci v obecném modelu soustavy ve tvaru

           

A vynásobíme-li celou rovnici zleva maticí , dostaneme redukovanou soustavu ve tvaru

           

S maticemi řádu m, kde

, ,

a vektorem buzení dimenze m

           

Je-li některá z matic  nesymetrická, doporučuje se také nesymetrická transformace typu

            , , , pro .

Za transformační matici můžeme vybrat modální submatici , složenou z m vlastních vektorů konzervativního modelu soustavy. Pohybová rovnice potom přejde do travu

            ,

kde

           

V případě, že se jedná o slabě nekonzervativní soustavu, přejde redukovaný model do tvaru

           

S diagonálními maticemi

           

            .

 

6.2 Guyanova redukce (Statická redukce)

 

Jedná se o velmi rozšířenou metodu. Spočívá v rozdělení počtu stupňů volnosti na m tzv. master stupňů volnosti a tzv. slave stupňů volnosti, přičemž platí, že . Mezi tzv. slave stupně volnosti můžeme vybírat jen ty stupně volnosti, ve kterých nepůsobí žádné vnější budící síly.

Model soustavy se potom převede do tvaru

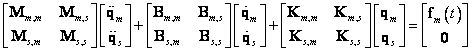                       kde matice typu  jsou symetrické řádu m, matice  jsou také symetrické rádu  a matice  jsou řádu  a obecně nemusí být symetrické.

Rozepíšeme-li druhý řádek v předchozí rovnici a zanedbáme-li setrvačné a tlumící síly, dostaneme tzv. kvazistatickou podmínku rovnováhy ve tvaru

           

Za předpokladu, že matice  je regulární, dostaneme

           

Tzv. slave souřadnice eliminujeme následující transformací

           

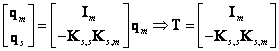
Matice redukovaného modelu pak mají tvar

           

kde a .  Redukovaná matice tuhosti je jednodušší a má tvar

            .

Transformovaný vektor buzení  je identický s původním.

Vzhledem k tomu, že pro odvození redukovaných matic bylo použito kvazistatické podmínky rovnováhy, je Guyanova redukce aplikovatelná na slabě tlumené soustavy, které splňují podmínku normy submatic matice hmotnosti

           

Této podmínky se dá dosáhnout výběrem tzv. master souřadnic, kolem kterých je soustředěna hmota. V případě diagonálně dominantních matic M a K posuzujeme příslušnost k tzv. master souřadnici podle velikosti poměru  vzhledem k nejvyšší očekávané frekvenci buzení . Pro  lze i-tou souřadnici zařadit mezi tzv. slave.

Guyanova redukce je velmi výhodná, sestavujeme-li model metodou konečných prvků hmotu umísťujeme jen do vybraných uzlů. Zobecnělé posuvy těchto uzlů jsou pak soustředěny do vektoru  a ostatní zobecnělé posuvy uzlů jsou soustředěny do vektoru . Potom je redukovaná matice hmotnosti ve tvaru

           

a při zanedbání tlumících sil, je kvazistatická podmínka rovnováhy splněna přesně. Redukovaný model

           

aproximuje m vlastních frekvencí a vlastních subrektorů vyhovující rovnící

            .

Vlastní vektory původního modelu dostaneme transformací

           

 

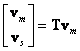
6.3 Parametrická redukce

 

Tato redukce je založena na nahrazení původního modelu o n stupních volnosti jednodušším, velmi časti diskrétním lineárním modelem předem dané struktury o menším počtu stupňů volnosti m. Cílem je opět výpočet parametrů náhradního modelu, tj. vlastních vektorů dimenze m, příslušející zpravidla frekvenčně nejnižším m vlastním frekvencím  původního neredukovaného modelu. Vlastní vektory  vzniknou z vlastních vektorů  vypuštěním souřadnic příslušející eliminovaným zobecněným souřadnicím. Zachovají se jen souřadnice odpovídající posuvům a natočeném vybraných uzlů konstrukce. Jsou to uzly, které:

-          mají mezi sebou vazby, jež se dále analyzují

-          jsou působišti budících sil

-          jsou místy soustředění hmoty

-          jsou místy lokalizace parametrů, které se dále analyzují

Princip metody je založen na splnění podmínek ortogonality vlastních vektorů redukovaného modelu

                       

kde  je Kroneckerovo delta. Dále předpokládáme symetrické matice redukované soustavy s  hmotnostních parametrech uspořádaných do vektoru m a s  tuhostních parametrech uspořádaných do vektoru k. Prvky matic  jsou lineárními funkcemi hmotnostních, resp. tuhostních parametrů. Proto existuje pro každý vlastní vektor  transformační vztahy

                       

kde m a k jsou hledané vektory hmotnostních resp. tuhostních parametrů. Matice  jsou typu , resp. .Jejich prvky jsou vyjádřeny pomocí souřadnic vlastních vektorů  pomocí vztahů

                        .

Zapíšeme-li tyto výrazy pro všechny možné kombinace i a j, dostaneme dvě soustavy algebraických lineárních rovnic

                       

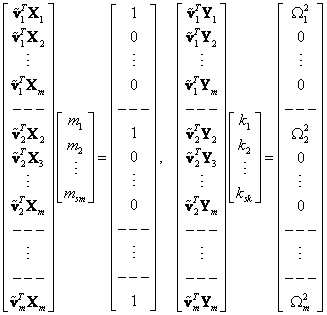
nebo také ve tvaru

                       

 

Matice  jsou typu  resp.  a bývají přeurčené. Řešení lze hledat jako minimum norem vážených reziduí

 

                       

Kde G je diagonální matice nezáporných váhových koeficientů. Těmito koeficienty je možno preferovat přesnost splnění některých podmínek ortogonality na úkor jiných. Z podmínek minima Euklidovských norem reziduí

 

                       

 

dostaneme dvě soustavy algebraických rovnic

 

                       

 

pro hledané hmotnostní, resp. tuhostní parametry redukovaného modelu. Podmínkou jejích řešitelnosti je regulárnost obdélníkových matic Φ a Ψ. Po stanovení parametrů redukovaného modelů, je účelné provést kontrolní výpočet jeho vlastních frekvencí a vlastních vektorů a ty porovnat s příslušnými hodnotami původního modelu. V případě špatné shody je možno provést ladění modelu pomocí váhových koeficientů v matici G, event. změnou struktury redukovaného modelu.

 

6.4 Metoda modální syntézy

 

V současné době se stále častěji setkáváme s úlohami modelování kmitání mechanických soustav s ložených z několika subsoustav navzájem spojených diskrétními pružně viskózními vazbami.

Každá subsoustava, izolovaná od ostatních, je charakterizována maticemi hmotnosti, tuhosti a tlumení, které mohou být obecně nesymetrické a můžeme je obecně zapsat jako součet jejich symetrické a nesymetrické části

 

         .

Kmitavý pohyb subsoustavy „j“ začleněného do soustavy pak lze vyjádřit v maticovém tvaru

           

kde vektor zobecněných souřadnic  je definován ve svém lokálním souřadnicovém systému. Vektor  představuje vnější buzení subsoustavy, vektor  představuje silové působení ostatních subsostav vázaných se subsoustavou „j“ pomocí pružně viskózních vazeb.

Dále mějme a , spektrální a modální matici konzervativní části modelu subsoustavy „j“

         .

Matice a splňují podmínky ortogonality

        

Množinu všech vlastních tvarů kmitu každé subsoustavy rozdělíme na  hlavních (master) tvarů a na množinu  vedlejších (slave) tvarů. Příspěvky hlavních tvarů se do dynamické odezvy soustavy budou započítávat, příspěvky vedlejších tvarů se započítávat nebudou. Přeskupíme-li pořadí všech vlastních tvarů tak, že na začátku modální matice bude  hlavních vlastních tvarů a pak budou následovat vedlejší tvary, potom můžeme modální a spektrální matici zapsat v následujícím tvaru

         .

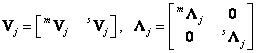Provedeme transformaci souřadnic

                  

kde  je vektor hlavních modálních souřadnic izolované subsoustavy „j“. Po pronásobení zleva maticí  dostaneme

                   .

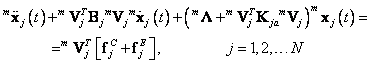Pro všechna j lze tento výraz přepsat do globálního tvaru

                  

kde

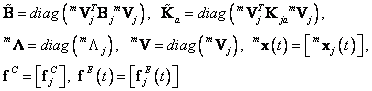
Globální vektor vazbových sil  je definován

                  

kde  je potenciální energie a  je disipativní energie funkce vazby mezi subsoustavami. U lineárních vazeb lze vektor vyjádřit pomocí matice tuhosti  a matice tlumení  ve tvaru

                   ,

kde  je vektor vnitřního kinematického buzení. V případě stacionárních vazeb je roven nule. Transformační vztahy se potom můžou vyjádřit ve tvaru

                        .

Dostáváme tak redukovaný model soustavy ve tvaru

                   .

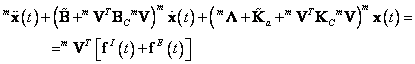Tato soustava je již řádu m. Počet stupňů volnosti m je roven součtu hlavních tvarů kmitu všech subsoustav. Metoda je dostatečně přesná při vhodném výběru hlavních tvarů kmitů a to i při značném snížení stupňů volnosti. Tento model lze následně použít pro další analýzy. Hlavní předností metody je to, že se sestavuje model na základě neúplného počtu vlastních hodnot konzervativních částí izolovaných subsoustav. Místo řešení problému vlastních hodnot soustavy o velkém počtu stupňů volnosti, řeší se několik problémů vlastních hodnot subsoustav. Subsoustavy se mohou řešit nezávisle ve svých lokálních souřadnicových systémech. Lze je řešit i každý v jiném výpočtovém prostředí. Využití takto redukovaného modelu je efektivní pro ladění a optimalizaci, které jsou založené na iteračních postupech nebo mnohonásobném opakování dynamické analýzy.

 

 

                                                                                                     

© Ústav mechaniky těles, mechatroniky a biomechaniky
Admin e-mail: krejci.p@fme.vutbr.cz

Poslední aktualizace