3 Základní teorie stability dynamických systémů

3.1 Stabilita ve smyslu Ljapunova

Relativně velkého počtu definic stability uvedeme jen nejdůležitější, které bezprostředně vycházejí ze základní myšlenky stability, formulované ruským matematikem Ljapunovem.

Uvažujeme nařízený dynamický systém, modelovaný rovnicí

 

                                                                                           (3.1)

 

nebo jedná-li se o autonomní systém, rovnicí

 

                                                                                              (3.2)

 

Budeme vyšetřovat podmínky, za kterých bude rovnovážný stav systému stabilní. O funkcích  předpokládejme, že jsou spojité a že mají spojité derivace podle proměnných . Nechť  představuje řešení stavové rovnice v čase t při počátečních podmínkách  v čase . Nejprve budeme definovat stabilitu rovnovážného stavu.

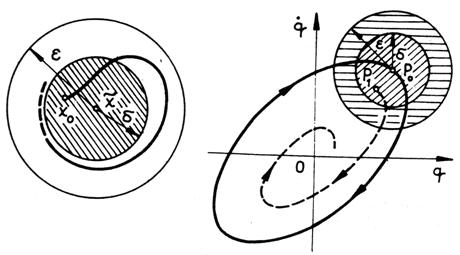
Obr. 3.1

 

Podle Ljapunova je rovnovážný stav  neřízeného dynamického systému stabilní, jestliže pro každou reálnou hodnotu  existuje takové reálné číslo , pro které platí, že při

 

                je                         pro                     (3.3)

Symbolem  je označena norma matice. Smysl tohoto tvrzení je patrný z obr. 31a. Rovnovážný stav je stabilní, když po malém vychýlení z tohoto stavu (vlivem „poruch“ amplitud nebo fází) zůstane trajektorie zastupujícího bodu systému v okolí  rovnovážného stavu. Podle této definice nemusí trajektorie zastupujícího bodu v čase nutně dosáhnout rovnovážného stavu , ale musí setrvat v předepsané blízkosti tohoto stavu.

Rovnovážný stav autonomního systému je asymptoticky stabilní, je-li stabilní ve smyslu Ljapunovy definice a každý pohyb, vycházející ze stavu , dostatečně blízkého stavu , konverguje v čase  ke stavu

Stabilitu periodického řešení budeme chápat jako stabilitu pohybu podél určité trajektorie, kterou je v případě periodických řešení limitní cyklus. Sledujeme, zda bod P₁ (reprezentující okamžitý stav systému), který se pohybuje po trajektorii blízké limitnímu cyklu, zůstává trvale ve zvolené oblasti , která obsahuje oblast viz obr. 3.1b. Bod P₀, reprezentující střed oblastí  i , se přitom pohybuje po limitním cyklu. Zůstává-li pro každé  bod P₁ trvale v oblasti, je periodické řešení ve smyslu Ljapunovovy definice (3.3) stabilní.

Při analýze stability odezvy řízených (buzených) systémů je minimálním požadavkem pro stabilitu ohraničený vstup a výstup a stabilita periodického řešení neřízeného systému (včetně stability počátečních podmínek).

 

3.2 Určování podmínek stability pro rovnovážné stavy systémů

 

Uvažujeme autonomní dynamický systém, popsaný stavovou rovnicí (3.2), kterou lze rozepsat na soustavu rovnic

                                               (3.4)

 

kde  jsou obecně nelineární funkce. Hodnoty rovnovážných stavových veličin  dostaneme jako řešení soustavy rovnic

 

                                                      (3.5)

 

Nyní definujeme poruchy  jako malé odchylky od rovnovážného stavu. Pohyb systému kolem rovnovážných hodnot stavových veličin pak definují rovnice:

 

                    (3.6)

 

Podle Ljapunovovy definice asymptotické stability bude rovnovážný stav systému stabilní, budou-li splněny relace  pro všechny i. Dosadíme vztahy (3.6) do rovnic (3.5). Po rozvinutí funkcí  do Taylorových řad v okolí hodnot  a po zanedbání vyšších členů rozvojů od druhého řádu výše, dostaneme soustavu rovnic

 

 

nebo stručně v maticovém zápisu

 

                                                                                                  (3.7)

 

kde , kde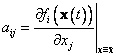

Řešení soustavy (3.7) je známé a rovno ; po jeho dosazení do (3.7) a po vyloučení triviálního řešení dostaneme maticovou formulaci problému vlastních hodnot matice A:

 

                                                                                               (3.8)

 

Jak je známo, tato rovnice má netriviální řešení tehdy a jen tehdy, je-li determinant matice soustavy roven nule. Ljapunov dokázal, že rovnovážný stav systému, charakterizovaný hodnotami  je stabilní, jsou-li reálné části všech vlastních hodnot  záporné, tj. když platí

 

                                                                              (3.9)

 

Splnění nerovnosti (3.9) je totožné s požadavkem záporného znaménka reálných částí všech kořenů tzv. charakteristické rovnice, definované jako

 

                                                                                             (3.10)

 

kterou lze rozepsat do tvaru

 

                                                                            (3.11)

 

Aby nebylo zapotřebí často pracně počítat kořeny polynomu (3.11), byla sestavena kritéria, podle nichž lze určit znaménka.

Podle Routh-Hurwitzova kritéria budou mít reálné části kořenů charakteristické rovnice záporné znaménka, budou-li:

·        všechny koeficienty charakteristické rovnice kladná čísla;

·        budou-li splněny následující determinantní nerovnosti:

 

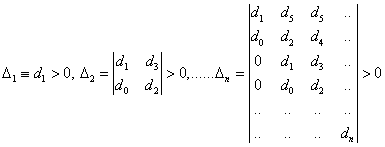         (3.12)

Pro systémy s větším počtem stupňů volnosti je analýza vlastností determinantů (3.12) dosti nepřehledná. Hledaly se proto jednodušší formulace. Tak například podle Liénardova kritéria postačí – při splnění prvé Routh – Hurwitzovy podmínky – aby byly splněny „pouze“ následující determinantní nerovnosti:

 

                                                                      (3.13)

 

kde determinanty  jsou definovány stejně jako v rovnici (3.12). Ilustrujme si vyloženou problematiku následujícím příkladem.

Analyzujme činnost gyroskopického stabilizátoru polohy, znázorněného na obr. 3.2. Na rám 2 nechť působí vnější moment , který má být ve svých účincích na gyroskop kompenzován pomocí momentu  vyvozovaného motorem 4. Toho se dosáhne tím, že potenciometr P, jehož kontakt C se otáčí spolu s osou 0₁, oddělí napětí, které se zesiluje v zesilovači Z a přivádí se na svorky motoru. (je-li kontakt C v neutrální poloze, je  a také ). Tlumící moment je roven  (R - Rayleighova konstanta).

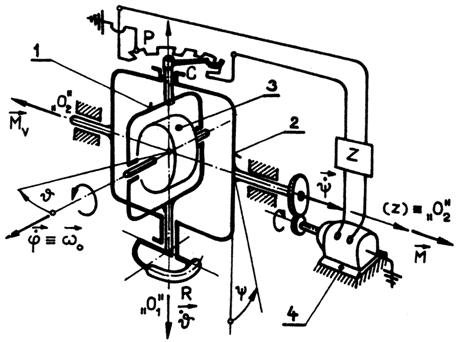
Obr. 3.2

 

Pohybové rovnice gyroskopického systému na obr. 3.2 jsou:

 

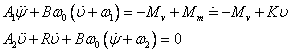                                             (3.14)

 

kde význam označení je stejný jako v technických rovnicích gyroskopu a ω₁, ω₂ jsou úhlové rychlosti rámu 1 a 2. Doplníme-li rovnice (3.14) identitou , lze zapsat ve tvaru stavové rovnice řízeného dynamického systému:

 

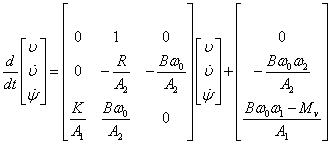                                               (3.15)

 

Rovnovážné řešení dostaneme, položíme-li stranu rovnice (3.15) rovnu nule. Tím dostaneme soustavu algebraických rovnic, která má řešení:

 

                                                                            (3.16)

 

Systém se ustálí na výchylce, která může být nulová v případě, že . Koeficienty  matice A, viz rov. (3.7), budou:

 

                               

 

Charakteristická rovnice typu (3.11) bude

 

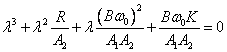                                                                         (3.17)

 

a je zřejmé, že její koeficienty jsou kladné (je to nutné i z fyzikálních důvodů). Z determinantních nerovností (3.12) pak plynou následující podmínky:

 

                                                                       (3.18)

 

Na základě rozboru výsledků (3.18) lze tedy učinit závěr, že vhodnou volbou tlumící konstanty R lze vždy dosáhnout stability řešení. Netlumený systém by byl nestabilní. Aby se u skutečných systémů tohoto typu eliminoval vliv úhlové rychlosti ω₁ na výchylku , užívá se dvou stejných gyroskopů, uložených rovnoběžně ve společném rámu. Pohyb těchto gyroskopů pak je mechanicky vázán.

Výsledky analýzy stability se uplatňují i ve speciálních odvětvích dynamiky systémů, například v teorii regulace. Jako příklad uvedeme Hartnellův regulátor, znázorněný na obr. 3.3.

 

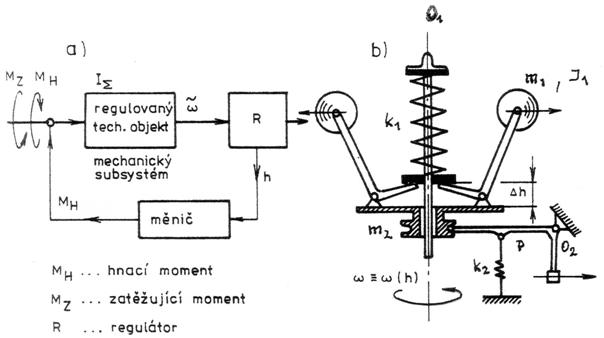
Obr. 3.3

 

Parametry potřebné pro výpočet jsou znázorněny ve výpočtovém schématu a představují: m₁ hmotnost vyvažovacího závaží, I₁ moment setrvačnosti úhlové páky včetně závaží k ose 0₁, I₂ moment setrvačnosti páky P k ose 0₂, m₂ hmotnost přestavovací objímky, k₁ tuhost pružiny regulátoru a k₂ tuhost vyrovnávací sílu regulátoru zanedbáme.

Okamžitou hodnotu kinetické energie můžeme vyjádřit

 

               (3.19)

 

když jsme položili

 

                       

 

Potenciální energie systému, označíme-li předpětí v pružinách s₁ a s₂, definuje rovnice:

 

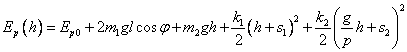                            (3.20)

 

Dosadíme-li vztahy (3.19) a (3.20) do Lagrangeovy rovnice II. druhu

 

                       

 

dostaneme pohybovou rovnici regulátoru:

 

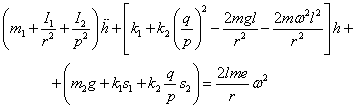                                         (3.21)

 

Tato rovnice je nelineární, neboť obě proměnné, h i ω, v ní vystupují v součinu. Omezíme-li se na vyšetřování „malých“ výchylek kolem rovnovážné polohy , tj. vyšetřujeme-li pohyby

 

                            (3.22)

 

lze rovnici (3.21) linearizovat. Regulační proces linearizovaného systému je totiž mnohem jednodušší a lze jej přehledně sledovat pomocí blokového schématu na obr. 3.3c. Nechť se regulované zařízení otáčelo v čase  úhlovou rychlostí . Když na ně v čase  začne působit brzdný moment , změní se otáčky o Δω a objímka regulátoru se posune z rovnovážného stavu o Δh. Posuv objímky způsobí prostřednictvím měniče zvětšení rychlosti hřídele regulátoru, na který začne působit hnací moment M_H(t). Veličiny Δω, Δh a moment M_H(t) jsou funkcemi času a jejich vzájemnou souvislost můžeme vyjádřit simultánními diferenciálními rovnicemi

 

                                                                       (3.23)

 

kde I_Σ je momentem setrvačnosti hmot, rotujících s hřídelem regulátoru a A, B, C, K jsou konstanty. Přitom druhou rovnici soustavy (3.23) definujeme na základě rovnice (3.21).

Derivujeme-li nyní druhou rovnici soustavy (3.23) podle času a dosadíme-li ji za Δω do prvé rovnice, dostaneme s ohledem na třetí rovnici (3.23) a po úpravě:

 

                                        (3.24)

 

Tři integrační konstanty, nutné pro řešení této rovnice, získáme z počátečních podmínek, například . Charakteristická rovnice modelu (3.24) má pak tvar

 

                                                                             (2.25)

 

O řešení rovnic typu (3.25) je známo, že mají vždy jeden kořen reálný. Podmínkou stability řešení je, aby rovnice (3.25) měla všechny kořeny reálné záporné nebo jeden kořen reálný záporný a dva kořeny sdružené s reálnou zápornou částí. Výběr parametrů systému, za kterých je těmto požadavkům vyhověno, pak určíme na základě rozboru Routh-Hurwitzových podmínek.

© Ústav mechaniky těles, mechatroniky a biomechaniky
Admin e-mail: krejci.p@fme.vutbr.cz

Poslední aktualizace