4 Řešení odezev dynamických systémů ve fázové rovině

4.1 Základní pojmy teorie fázové roviny

 

Mnohé problémy analýzy dynamických systémů vedou k řešení diferenciální rovnice

 

                                                                                               (4.1)    

 

kde  je obecně nelineární funkce výchylek x a rychlostí . Přiřadíme-li ke každé výchylce x její rychlost (tj. derivaci) ve stejném čase, bude v tomto časovém okamžiku definován stav systému a také jeho zobrazení v tzv. fázové rovině . Polohu systému ve fázové rovině pak určuje tzv. zastupující bod.

Zavedením nové proměnné  můžeme přenést rovnici (4.1) na soustavu dvou rovnic prvého řádu

 

                                                                                  (4.2)

 

nebo obecně

 

                                                                          (4.3)

 

což je nejjednodušší forma stavového prostoru. Pokud funkce P(x,y) a Q (x,y) neobsahují přímo čas t, mluvíme o systému autonomním, v opačném případě mluvíme o systému neautonomním.

Ve fázové rovině – resp. – pohyb modelu reálného dynamického systému zobrazuje fázová křivka jejíž diferenciální rovnici získáme, vyloučíme-li z rovnic (4.3) čas t:

 

                                                                                                 (4.4)

 

Na základě takto formulované fázové křivky lze fázový prostor rozložit na všechny možné trajektorie; takovu množinu možných fázových dřivek pak nazýváme fázovým portrétem dynamického systému. Rychlost, se kterou se po fázové křivce pohybuje zastupující bod, nazýváme fázovou rychlostí:

 

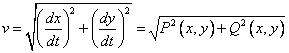                                                (4.5)

 

Zrychlení je pak dáno vztahem

 

                                                                                    (4.6)

 

Z rovnice (4.4) je zřejmé, že rovnice fázové trajektorie neobsahuje přímo čas. Máme-li ale vypočítat dobu pohybu zastupujícího bodu mezi dvěma body A a B, postupujeme takto:

 

                                                                   (4.7)

 

Základní význam mají ty body roviny (resp. fázové křivky), ve kterých je fázová rychlost nulová. Tyto body nazýváme zvláštními nebo také singulárními body. Fyzikální význam singulárních bodů spočívá v tom, že reprezentují rovnovážné stavy dynamických systémů. Určení polohy těchto bodů ve fázové rovině vyplývá z rovnice (4.5); aby bylo v = 0, musí platit:

 

                             a                                                   (4.8)

Obr. 4.1

 

Ostatní body fázové roviny, ve kterých je v ≠ 0, nazýváme regulárními. Každým regulárním bodem může procházet pouze jedna fázová trajektorie. Fázové křivky respektují určitá pravidla:

·        v horní polovině () se zastupující bod pohybuje po libovolné fázové křivce zleva doprava, v dolní polovině () naopak;

·        v regulárních bodech, které leží na ose [x], protínají fázové křivky tuto osu pod pravými úhly;

·        v regulárních bodech, které neleží na ose [x], nemůže mít fázová trajektorie tečnu rovnoběžnou s osou [x];

·        pokud jakákoliv spojitá fázová trajektorie protíná osu [x] ve dvou regulárních bodech, leží mezi těmito body nanejvýše jeden singulární bod;

·        periodickým režimům pohybu systému odpovídají uzavřené fázové křivky, které neprocházejí zvláštními body. Doba pohybu zastupujícího bodu po takové křivce odpovídá periodě pohybu.

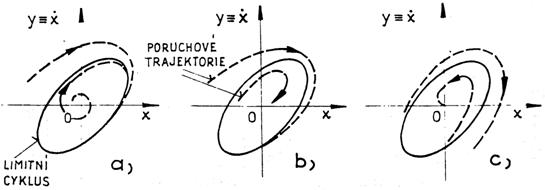
Struktura základních typů fázových křivek v blízkosti singulárních bodů, při rovnovážných stavech, je patrná z tabulky tab. 1. Rozeznáváme čtyři základní typy singulárních bodů: stabilní „střed“, nestabilní „sedlo“, a „ohnisko“ a „uzel“, které mohou být stabilní i nestabilní. Izolované uzavřené fázové křivky, odpovídající rovnovážným stavům autonomních systémů, nazýváme limitní cykly. Působením vnější poruchy se zatupující bod vychýlí z dráhy podél limitního cyklu a pohybuje se po tzv. poruchové trajektorii. Směřují-li poruchové trajektorie z obou stran k limitnímu cyklu, je limitní cyklus stabilní (obr. 4.1a), směřuje-li poruchová trajektorie k limitnímu cyklu jen z jedné strany, je cyklus polostabilní (obr. 4.1b), vzdalují-li se poruchové trajektorie od limitního cyklu na obou stranách, je příslušný cyklus nestabilní (obr. 4.1c).

 

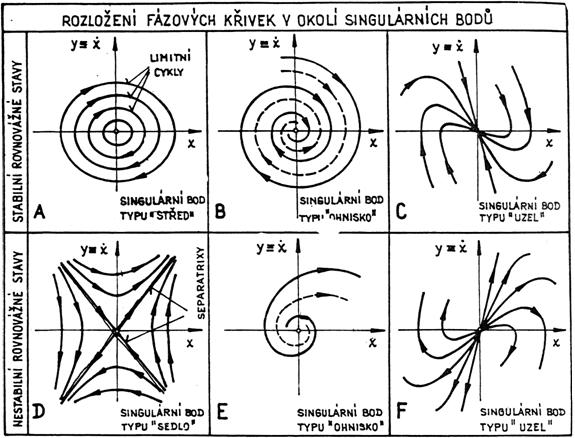
Tabulka 2

 

Izolované fázové trajektorie procházejí „přes“ singulární body typu „sedlo“, se nazývají separatrixy – viz tabulka tab. 2, obr. D. Pohyb mechanického systému, odpovídající pohybu zastupujícího bodu po separatrixách je nestabilní a fyzikálně neralizovatelný. Důležité však je, že separatrixy rozdělují fázovou rovinu na oblasti počátečních podmínek, odpovídajících principálně rozdílným typům pohybů systémů (rezonanční resp. nerezonanční pohyby).

Z obrazů fázových trajektorií v okolí zvláštních bodů tedy můžeme vyhodnotit nejen trajektor pohybu systému, ale objasnit i otázku stability rovnovážných stavů.

 

 

4.2 Příklady dynamické analýzy jednoduchých systémů

Příklad A1:

Analyzujte chování netlumeného harmonického oscilátoru ve fázové rovině. Rovnice harmonického oscilátoru, který je modelem dynamických systémů má tvar:

 

                                                                                                     (4.9)

 

lze ji nahradit soustavou rovnic typu (4.3), dosadíme-li za  a . Odpovídající rovnice fázové trajektorie je

 

                       

 

nyní přepíšeme tuto rovnici do tvaru, který lze snadno integrovat:

           

                       

 

a integrací dostaneme

 

                         C je integrační konstanta                                 (4.10)

 

Obrazem této rovnice ve fázové rovině jsou elipsy, které představují jednotlivé trajektorie pro různé hodnoty konstanty C, jak je to patrno z tabulky tab. 2, obr. A. Pro  degeneruje elipsa (viz. 2) v bod o souřadnicích . Protože právě v tomto bodě jsou splněny podmínky (4.8), jedná se o singulární bod. V tomto případě singulárním bodem neprochází žádná z fázových trajektorií, pouze jej obalují. Singulární bod tohoto typu nazýváme „středem“. Rychlost zastupujícího bodu vypočítáme podle vztahu (4.5):

                       

                       

 

Je zřejmé, že nulovou bude tato rychlost jen v singulárním bodě. Můžeme tedy vyslovit následující závěr: analyzovaný systém může vykonávat stabilní periodické pohyby při libovolných počátečních podmínkách s výjimkou případu, kdy .

 

Příklad A2:

Analyzujme chování harmonického oscilátoru s malým vazkým třením a nakreslete odpovídající fázovou trajektorii.

V tomto případě analyzujeme rovnici

 

                       

 

Pomocí rovnic (4.3), kde  a , sestavíme diferenciální rovnici fázových trajektorií:

 

                                                                                                         (4.11)

 

Pro usnadnění integrace rovnice (4.11) je vhodné zavést substituci . Pak lze psát  a po dosazení těchto vztahů do (4.11) dostaneme:

 

                       

 

Z tohoto vztahu můžeme vyjádřit

 

                       

 

respektive

 

                       

 

Po integraci této rovnice získáme výraz

 

                       

 

kde C je opět integrační konstanta. Umocníme-li tento výraz a přejdeme-li k původním souřadnicím x a y dostaneme

 

                                                        (4.12)

 

Kde . Rovnici (4.12) přísluší opět rodina fázových křivek, které vyplňují fázovou rovinu. O jaký typ křivek jde, zjistíme snadno následujícím postupem. Položíme a . V souřadnicích ρ, φ (polárních) přejde rovnice (4.12) do tvaru

 

                                                                                                                     (4.13)

 

ze kterého je zřejmé, že fázové křivky představují spirály, směřující k počátku , který se v tomto případě nazývá stabilním ohniskem, viz tabulka tab. 2 (obr. B). Počátku ovšem nemůže být dosaženo v konečném čase. Rychlost zastupujícího bodu, pohybujícího se po těchto fázových křivkách, je . Pohyb systému v tomto případě směřuje asymptoticky k rovnovážnému bodu, ve kterém ustane.

 

Příklad A3:

Analyzujte chování harmonického oscilátoru se suchým třením a nakreslete odpovídající fázovou trajektorii.

Uvážíme-li vliv suchého tření, lze pohybovou rovnici harmonického oscilátoru zapsat ve formě

 

                        , kde                                         (4.14)

 

Zavedeme novou proměnnou  a můžeme psát:

 

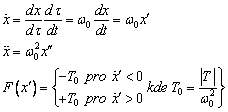                                                                           (4.15)

 

S ohledem na substituce (4.15) přejde pohybová rovnice (4.14) do tvaru

 

                                                                                                         (4.16)

 

A nyní již lze analyzovat stejně jako v přechozích úlohách. Položíme tedy  a , sestavíme diferenciální rovnici fázových trajektorií

 

                                                                                                           (4.17)

 

a upravíme ji do tvaru

 

                                                                                                            (4.18)

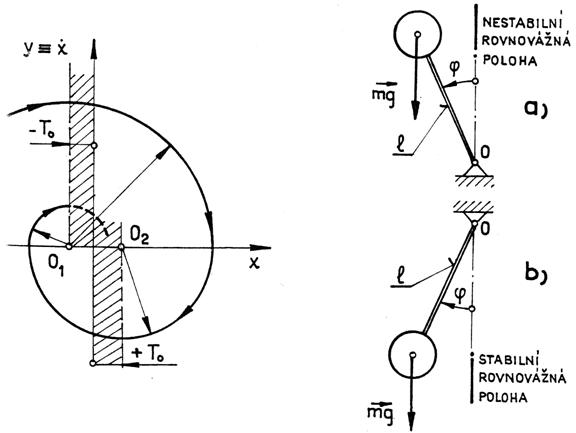
Obr. 4.2                                                                       Obr. 4.3

 

Po integraci dostaneme rovnici kružnice (viz obr. 4.2) se středem v bodě O souřadnicích  a . Pro je (bod O₁), pro  je  (bod O₂). Fázová křivka se tudíž bude skládat z částí kružnic opsaných kolem středů O₁ a O₂. Oblast mezi body O₁ a O₂ představuje tzv. pásmo necitlivosti, fyzikálně charakterizované tím, že v tomto pásmu je síla pružná menší než síla třecí. To znamená, že dostane-li se systém do tohoto pásma (zastupující bod bude na čarkované části fázové křivky), jeho pohyb ustane, aniž by blo dosaženo počátku souřadnic (stabilního ohniska).

 

Příklad A4:

Sestavte tzv. fázový portrét pohybu matematického kyvadla, znázorněného na obr. 4.3.

 

a) Pohyb v okolí nestabilní rovnovážné polohy

Omezíme-li se na malé kmity kyvadla kolem nestabilní rovnovážné polohy (obr. 4,3a), má pohybová rovnice tvar

 

                                                                                            (4.19)

 

kde

Po dosazení  a  , kde  do (4.19) získáme opět diferenciální rovnici fázových trajektorií:

 

                                                                                                                     (4.20)

 

Po integraci této rovnice dostaneme rovnice hyperbol, zaplňujících fázovou rovinu:

 

                        , C je integrační konstanta                                               (4.21)

 

Pro degeneruje rovnice (4.20) v soustavu dvou přímek , které prochází zvláštním bodem . Při hyperboly zvláštním bodem neprocházejí, pouze se asymptoticky přibližují k přímkám , které nazýváme „separatrixy“. Pohyb po separatrixách je tedy fyzikálně neuskutečnitelný. Fázová rychlost zastupujícího bodu bude rovna  a nulové hodnoty dosáhne pouze ve zvláštním bodě o souřadnicích , který se v tomto případě nazývá „sedlem“ (viz tabulka tab. 2, obr. D). Pohyb systému je v tomto případě nestabilní.

 

b) Pohyb v okolí stabilní rovnovážné polohy

Rovnice matematického kyvadla nyní je

 

                                                                                              (4.22)

 

Funkce  a diferenciální rovnice fázových trajektorií po separaci proměnných je rovna

 

                       

 

Po částečné integraci dostaneme:

 

                                                                                       (4.23)

 

kde E_P je potenciální energie a C je integrační konstanta. Z rovnic (4.23), představující zákon zachování mechanické energie lze zjistit, že každé skupině počátečních podmínek (0) přísluší jediná hodnota C₀, ale každé jiné hodnotě odpovídá nekonečně mnoho hodnot x a y.

Pro model popsaný rovnicí (4.22), přejde rovnice (4.23) po integraci do tvaru

 

                                                                                                         (4.24)

 

Funkce  má izolovaná minima v bodech , viz
obr. 4.4a. Těmto minimům odpovídají ve fázové rovině () stabilní zvláštní body – středy. Při  má funkce E_P(φ) izolovaná maxima, kterým odpovídají nestabilní zvláštní body – sedla. Celkový obraz fázových křivek v rovině () je na obr. 4.4b.

 

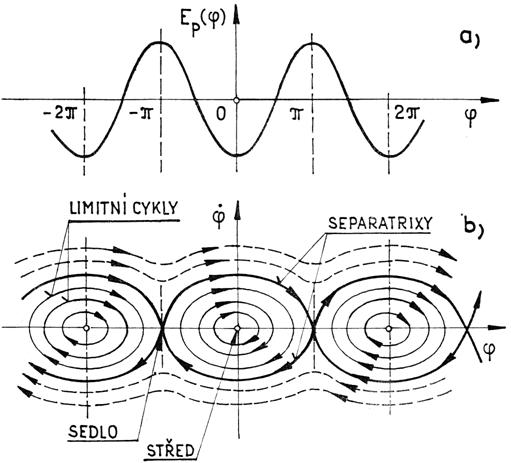
Obr. 4.4

 

Z rozboru rovnice (4.24) vyplývají zajímavé důsledky, týkající se možných pohybů modelu (4.21). Pro  reálný pohyb neexistuje. Pro hodnoty  představují fázové trajektorie izolované uzavřené křivky, situované kolem stabilních singulárních bodů – středů, které odpovídají možným periodickým pohybům. Při  se fázové trajektorie protínají na ose [φ] v nestabilních singulárních bodech – sedlech; víme již, že tyto křivky představují separatrixy. Pokud bude , odpovídá pohyb zastupujícího bodu po neuzavřených křivkách rotačnímu pohybu kyvadla v jednom směru.

U složitějších dynamických modelů, především nelineárních, jsou fázové obrazy mnohem složitější, viz tabulka tab. 3; ovšem základní informace o charakteru pohybu zastupujícího bodu ve fázové rovině zůstávají v platnosti.

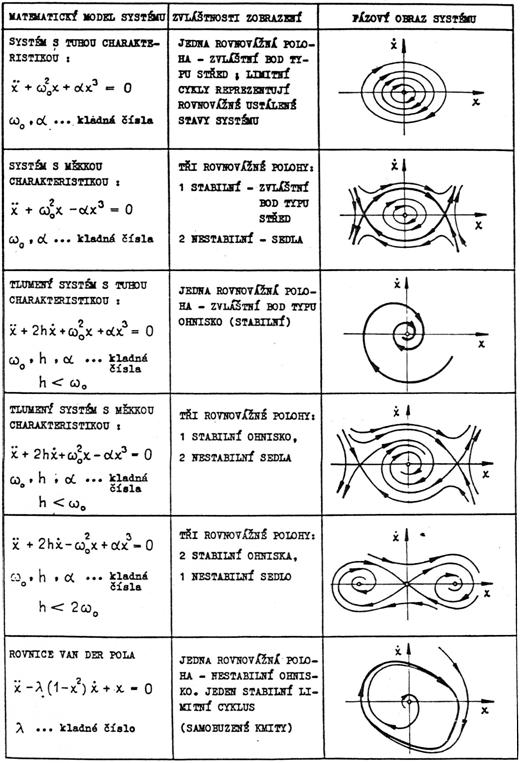
Tabulka 3

© Ústav mechaniky těles, mechatroniky a biomechaniky
Admin e-mail: krejci.p@fme.vutbr.cz

Poslední aktualizace