1. Lineární dynamické systémy

1.1 Rezonanční charakteristiky lineárních systémů s jedním stupněm volnosti

Závislost amplitudy vynucených kmitů na frekvenci nazýváme amplitudo-frekvenční charakteristikou. Podobně změnu fázového posunutí (u tlumených soustav) na frekvenci nazýváme fázové charakteristiky. Tyto charakteristiky považujeme u mechanických systémů za základní a snadno je odvodíme na základě rozboru odezvy soustavy buzeného harmonickou silou.

 

Matematickým modelem soustavy je známá rovnice

 

                                                   (1)

 

kde m, b a k představují hmotnost, součinitel viskózního tlumení a součinitel tuhosti. Pro harmonické buzení   bude odezva rovněž harmonická.

 

                                                    (2)

 

kde A a y jsou amplituda a fázové posunutí (zpoždění odezvy na buzení). Po dosazení za sílu ado rovnice (1) a po eliminaci triviálního řešení dostaneme vztah

 

                                                        

 

ze které již snadno určíme závislost absolutních velikostí amplitudy a fáze na budící frekvenci w, tj. amplitudovou a fázovou frekvenční charakteristiku

 

                (3)

 

Užijeme – li pojmy: , dynamické zesílení , vlastní frekvence , frekvenční naladění  a poměrný útlum , přejdou vztahy (3) do bezrozměrného tvaru:

 

 ,                                    (4)

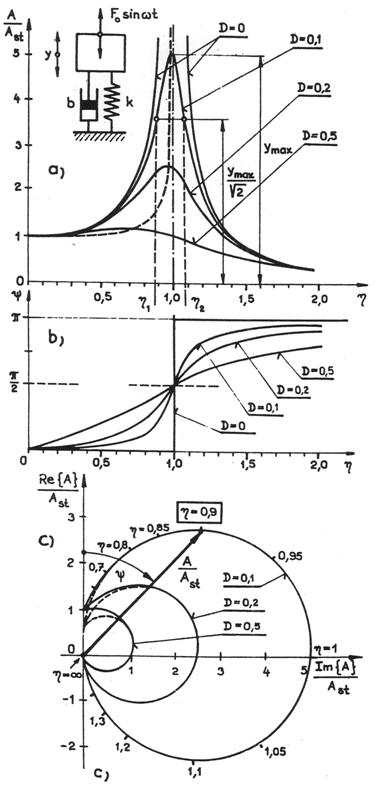
Obr.1.1

 

Rezonanční křivky popisují vynucené kmitání všech lineárních tlumených systémů s jedním stupněm volnosti, lze v bezrozměrných souřadnicích znázornit jednoparametrickou soustavu křivek (parametr D), které jsou znázorněny na obr.1.1 (amplitudové rezonanční křivky). Křivky pro  odpovídají rezonančním charakteristikám netlumené soustavy.

Z rozboru charakteristik můžeme získat řadu informací. Z prvé rovnice (4) lze snadno zjistit, že pro  je a pro všechna D. Ze stejné rovnice lze vypočítat i výšku a polohu rezonanční křivky. Frekvenční naladění , při kterém je amplituda vynucených periodických kmitů maximální je definováno vztahem . To znamená, že vrcholy rezonančních amplitudových křivek se z rostoucím tlumením posouvají k nižším frekvencím, jejich „výška“ se snižuje a pro přechází rezonanční křivka do monotónně klesající závislosti s maximem v bodě  (viz. obr.1.1 čárkovaný průběh).

U málo tlumených soustav naopak leží rezonanční vrchol v blízkosti přímky , reprezentujíci stav kdy . Z prvé rovnice (4) pak můžeme pro tento stav vypočítat, že  což je hodnota na základě které lze z naměřených charakteristik určit odhady D a pak i součinitele tlumení .

V technické praxi tyto hodnoty zcela postačují a proto také velikosti maximálních výchylek odhadujeme dostatečně přesně podle vztahu

 

      pro                                                                  (5)

 

S velikostí tlumení souvisí také šířka vrcholu rezonanční amplitudové křivky, definovaná jako rozdíl souřadnic  určených průsečíky rezonanční křivky s vodorovnou přímkou na úrovni

Dosadíme-li opět toto řešení spolu s buzením  do pohybové rovnice, dostaneme po úpravě soustavu rovnic pro určení reálné a imiaginární složky odezvy:

 

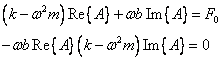                                                  (8)

 

Tuto soustavu převedeme nejprve do tvaru, obsahujícího bezrozměrné parametry η a D:

 

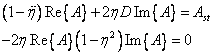                                                                 (9)

 

Nyní provedeme následující úpravy: prvou rovnici soustavy (9) vynásobíme hodnotou Im{A} a odečteme od ní druhou rovnici téže soustavy, vynásobenou Re{A}. Po úpravě dostaneme:

           

                                                                 (10)

Dále budeme sledovat průběh rozonanční křivky v blízkosti rezonance. Uvážíme-li, že může dojít k malému „rozladění“ od přesné hodnoty rezonance, můžeme místo naladění η dosadit do rovnice (10) a do druhé rovnice (9) hodnotu . Po zanedbání vyšších mocnin malé hodnoty Δ dostaneme soustavu dvou rovnic, ze kterých po eliminaci hodnoty Δ dostaneme:

 

                                                           (11)

 

Rovnice (11) představuje v rovině, určené souřadnicemi  a  kružnici, která prochází počátkem (Re{A}=Im{A}= 0) a má střed v bodě o souřadnicích a , viz obr. 1.1c. Na tomto obrázku jsou zakresleny dvě kružnice, pro poměrné útlumy D = 0,1 a D = 0,2. Plně jsou znázorněny přesné závislosti, získané numerickým řešením soustavy (9). Je zřejmé, že pouze při nízkých frekvencích buzení jsou odchylky přesných závislostí od kružnic (čárkované průběhy) patrné. Ovšem tyto diference se s klesajícími hodnotami tlumení dále zmenšují. Z Kennedy – Pancova diagramu, nazývaného také kruhovým diagramem je zřejmé, že z něj lze současně odečítat nejen zesílení , ale i fázové posunutí ψ pro dané naladění η. Je zapotřebí si ale uvědomit, že rychlost zde předbíhá výchylku o .

Z rozboru frekvenčních diagramů vyplývají, kromě určení vlastní frekvence, zesílení, případě poměrného útlumu i další významné skutečnosti, kterých lze využít v teorii přístrojů k zajištění rovnovážných stavů apod. Na hmotný bod totiž působí síly: budící síla F, pružná (vratná) síla , tlumící síla  a setrvačná síla . Tyto síly působí ve stejném směru, jen u netlumených systémů; u tlumených systémů je musíme sledovat Gaussově rovině, viz obr. 1.2a. Všechny tyto síly musí být v rovnováze a musí tudíž vytvářet uzavřený čtyřúhelník jehož tvar se bude měnit se změnou ω, resp. se změnou naladění . Typické tvary tohoto čtyřúhelníku jsou znázorněny na obrázcích 1.2b,c,d, představujících podrezonanční (), rezonanční () a nadrezonanční stav (). Z těchto vektorových obrazců lze vyvodit následující závěry o vlastnostech kmitajícího systému: při nízkých kmitočtech (podrezonančních) je budoucí síla zachycována hlavně reakcí pružného uchycení, zatím co tlumící a setrvačné síly jsou méně významné a způsobují malé, ale dobře patrné fázové posunutí (obr. 1.2b). S rostoucí frekvencí se tyto síly zvětšují a roste i úhel ψ, který v rezonoanci dosáhne hodny . Z obr. 1.2c je dále patrné, že budící síla je v rovnováze se silou tlumící a pružná síla je v rovnováze se silou setrvačnou. V nadrezonanční oblasti (obr. 1.2d) se fázové posunutí dále zvětšuje, amplituda kmitů klesá (viz obr. 1.1a) a s ní klesá i amplituda pružné síly. Dosti vysoko nad rezonancí pak přibližně platí , tj. vnější síla je zachována především setrvačností hmoty systémů. Elastické i tlumíci účinky jsou minimální, úhel se v limitě blíží k hodnotě π.

 

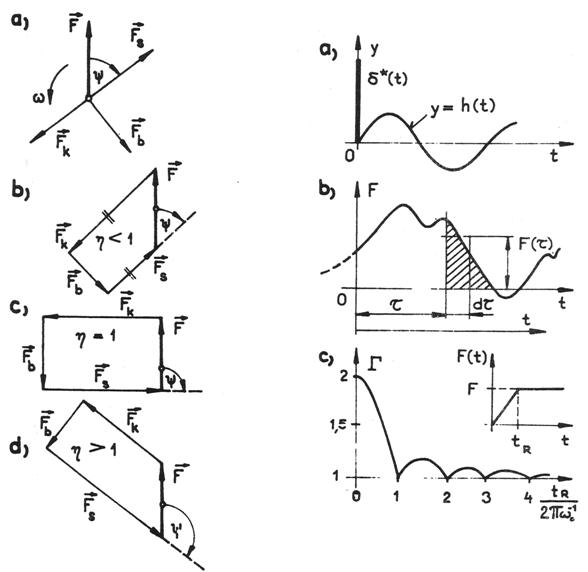
Obr. 1.2                                                         Obr. 1.3

 

Tyto vektorové obrazce slouží především k ujasnění fyzikálních poměrů v kmitajícím mechanickém systému. Nejsou ovšem v praxi tak rozšířené jako amplitudové a fázové charakteristiky, kruhové diagramy nebo odezvy na speciální typy budících funkcí, se kterými se seznámíme v následujícím odstavci.

 

 

1.2 Odezvy systémů na speciální typy budícíh funkcí

 

Nejznámější z těchto odezev je odezva na jednotkový impuls, krátce impulstní funkce. Uvažujeme systém, který byl v čase  v klidu a kterému je v čase  udělen jednotkový silový impuls , kde symbol  označuje známou Diracovu delta – funkci, která je všude nulová s výjimkou bodu , ve kterém platí

 

           

 

U netlumeného systému lze odezvu na jednotkový impuls vypočítat z podmínky změny hybnosti v elementárním čase:

 

Za dobu, pro kterou silový impuls působil, dojde ke změně rychlosti a ke změně polohy  (jde o malou veličinu druhého řádu):

 

                                             (16)

 

Po pohybovou rovnici netlumeného systému, zatíženého v čase t impulstní silou

                                                                     (17)

 

budou počáteční podmínky (s ohledem na to, že systém byl původně v klidu a s vyžitím vztahu (14) tyto:

 

 

Řešení rovnice (17) pak můžeme napsat ve tvaru

 

   (18)

 

zde  a funkce   představuje hledanou impulsní funkci. Je-li systém tlumený, bude impulsní funkce rovna

 

                                                                                               (19)

 

Pomocí impulsní funkce lze snadno určit odezvu systému na obecnou budící silu F(t), představíme-li si ji jako množinu elementárních obdelníkových impulsů , viz obr. 1.3a,b. Za předpokladu platnosti zákona superpozci platí pro netlumený systém

 

                               (20)

a pro tlumený systém

 

                                                   (21)

 

Rovnice (20) a (21) platí pro nulové počáteční podmínky.

Tab. 1

 

Periodické, harmonické nebo rezonanční kmitání je pouze zvláštním případem obecného pohybu systému, buzeného silou libovolného průběhu, o čemž se můžeme přesvědčit. Je známé, že u netlumeného systému, který je v rezonanci, nelze vypočítat odezvu pomocí vzorců (3). Lze ale použít rovnici (20), do které dosadíme za ; dostaneme výraz

 

 

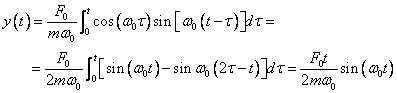
který představuje známé rezonanční kmitání, charakterizované amplitudou vzrůstající s časem, které odpovídí fyzikální skutečnosti.

Odezvu netlumeného lineárního systému na konstatní, periodické nebo skokového buzení lze vyjádřit také tím způsobem, že partikulární část odezvy upravíme do tvaru

 

                                                                                    (22)

 

kde funkce Γ představuje faktor zasílení, formulovaný jako funkce času. Rovnice charakterizující změnu Γ pro některé často užívané průběhy zatězujících účinků, jsou uvedeny v tabulce tab. 1. Z těchto vztahů lze jako extrémy určit i maximální hodnoty a čas (měřený od počátku působení impulsní síly), ve kterém je těchto maximálních hodnot dosaženo a to pouze v závisloti na vlastní frekvenci systému, kterou lze vhodnými zásahy do struktury systému měnit. Tyto údaje jsou v teorii přístrojů a řídích systémů velmi důležité, neboť vlastně určují „setrvačnost“, se kterou se přístroj (soustava) reaguje na daný impuls. Jeden z konkrétních průběhů faktoru zasílení je znázorněn na obr. 1.3c a je na něm dobře patrné doznívaní odezvy, vyvolané náhlou změnou budící síly. Skutečnost, že v tomto případě neuvažujeme tlumení, nemá praktický význam, pokud není extrémně vysoké.

 

1.3 Přenosová funkce. Konvoluce

 

Uvažujme dynamický systém popsaný rovnicí (1), který je buzen obecnou spojitou časovou funkcí f(t):

 

                                                                      (23)

 

Pokud tato rovnice splňuje podmínky Laplaceovy transformace, můžeme vyjádřit obrazy vstupů a výstupů takto:

 

                                                    (24)

                                                     (25)

 

Zde symbol (s) představuje komplexní proměnnou. Pro nulové počáteční podmínky () přejde rovnice (23) do jednoduchého tvaru

 

 

odkud již lze snadno vyjádřit obraz odezvy

 

                                                                      (26)

 

U reálných dynamických systémů splňují funkce buzení i odezvy současně také podmínky kladené na Fourierovu transformaci; můžeme tedy položit  a rovnice (26) přejde do tvaru:

 

                                      (27)

 

Kde  je přenosová funkce systému (23).

Přechod z frekvenční oblasti do oblasti časové lze uskutečnit pomocí inverzní Fourierovy transformace

 

                                        (28)

 

kde h(t) je impulstní funkce, definovaná rovnicí

 

                                                                           (29)

 

Symbol *, užitý v rovnici (24) představuje tzv. konvoluční součin nebo také Duhamelovy integrály. Aplikujeme-li nyní na rovnici (24) znovu Fourierovou transformaci, dostaneme opět rovnici (23):

 

           

 

Zavedeme-li nyní substituci , resp. , dostaneme

 

                                   (30)

Porovnáme-li rovnice (28) a (30) lez říci, že konvolace v časové oblasti a naopak (tzv. konvoluční teorém). Konvoluční integrály se využívají v mnoha inženýrských aplikacích a také v teorii náhodných kmitů, jak uvidíme později. Princip konvoluce je znázorněn na obr. 1.4. Předpokládáme, že každý bod křivky , můžeme považovat za impuls v hodnotě rovné hodnotě uvažovaného bodu, například , viz obr. 1.4a. Každý takový impuls vybudí odezvu systému (23) , jejíž velikost je úměrná hodnotě funkce  v uvažovaném okamžiku a jejíž počátek se shoduje s polohou budícího impulsu na časové ose. Na obr. 1.4c je silně vyznačena odezva, odpovídající impulsu . Je patrné, že tato odezva má počátek v čase tn a špičková hodnota se objeví až v čase , kde význam  je patrný z průběhu 1.4b.

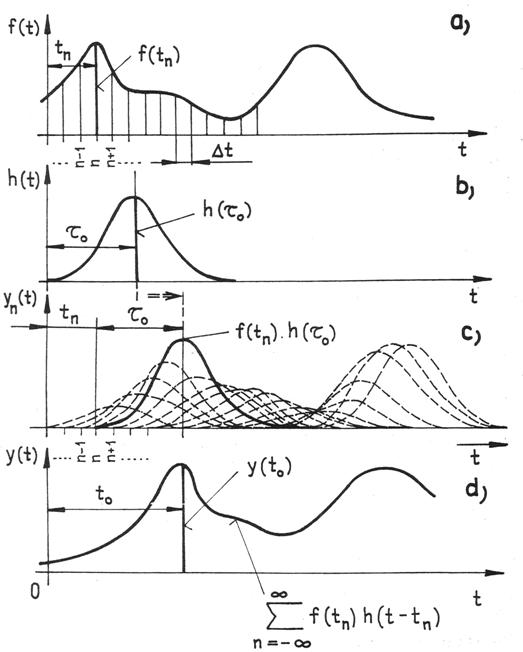
Obr. 1.4

 

Velikost špičkové hodnoty bude:  a hodnota odezvy v kterémkoliv jiném čase  bude definována analogicky: . Celková hodnota odezvy v čase  pak bude rovna součtu odezev na buzení počínající v různých časech, lišících se o krok , tj.:

 

           

 

Nyní již můžeme vyjádřit celkové hodnoty odezvy v libovolném čase :

           

           

 

Je zřejmé, že limitováním této rovnice pro  dojde k rovnici typu (28), což ilustruje obr. 1.4d.

 

1.4 Dynamické charakteristiky systémů o n stupnícho volnosti

 

Reálné mechanické soustavy lze obecně modelovat soustavu simultárních pohybových rovnic. Omezíme-li se na diskretizované modely, můžeme tuto soustavu zapsat ve tvaru maticové rovnice

 

                                                                         (32)

 

ke M,B,K jsou matice hmotností, tlumení a tuhostí, q(t) je časově proměnný vektor zobecněných výchylek a 0(t) je nulová matice.

K popisu vlastností systémů o více stupních volnosti používáme v podstatě stejných danamických charakteristik jako u systémů s jedním stupněm volnosti. Jsou to: spektra vlastních frekvencí a tvarů vlastních kmitů, matice impulstních funkcí a matice přenosových funkcí.

Spekra vlastních frekvencí a tvarů vlastních kmitů pro netlumené systémy lze souhrnně vyjádřit prostřednictvím spektrální matice  a modální matice U:

 

                  (33)

 

kde , jsou vlastním frekvence a sloupce v matici U představují odpovídající vektory.

Pro tlumené systémy definujeme rovněž spektra vlastních frekvencí  a tvarů vlastních tlumených kmitů , tentokrát jako výsledek řešení tzv. komplexního problému vlastních hodnot

           

                                                                                (34)

 

Pro malá tlumení lze využít s výhodou následujících vztahů:

 

                                              (35)

 

kde  je reálná a  imaginární část komplexního vlastního čísla , je r-tá vlastní frekvence netlumeného systému a  součinitel poměrného tlumení, příslušný r-tému tvaru kmitu, vypočtený pomocí vzorce

 

                                                                             (36)

 

když  je r-tý vlastní vektor, tj. r-tý sloupec modální matice U. Vlastní vektory tlumeného systému jsou rovněž komplexní, mají reálné a imaginární části, avšak pro slabě tlumené systémy platí:

           

                                                                                (37)

 

kde  jsou opět r-té sloupce komplexní modální matice V.

Matice přenosových funkcí   je definována analogicky k rovnici (27):

 

                                                                                   (38)

 

Při výpočtu matice impulsních odezvových funkcí  lze využít skutečnosti, že matice  a  jsou vázány vztahy přímé a zpětné Fourierovy transformace; tedy:

 

                                             (39)

 

Známe-li hodnoty prvků matice , můžeme vypočítat odezvu systému o n stupních volnosti na obecnou budíci sílu  pomocí rovnice

 

                                                                      (40)

 

stejně jako její obraz ve frekvenční rovině

           

                                                      (41)    

 

kde  je vektor počátečních výchylek a  je Fourierovský obraz budícího vektoru ve frekvenční oblasti. Stejně lze definovat i konvolutorní součin v maticové formě

 

                                                                  (42)

 

který je analogický k rovnici (28).

Přenosové a impulstní charakteristiky lze definovat i pro systémy elektrické či elektronické, hydraulické apod.

© Ústav mechaniky těles, mechatroniky a biomechaniky
Admin e-mail: krejci.p@fme.vutbr.cz

Poslední aktualizace