2. Základy teorie diskrétních dynamických systémů

 

Obecně jsou úlohy dynamiky strojů popsány parciálními diferenciálními rovnicemi v prostorových souřadnicích a čase. Vhodnou diskretizací prostoru, ať již subjektivní, nebo založenou na metodě konečných prvků, lze danou úlohu převést na systém obyčejných diferenciálních rovnic zapsaných maticově ve tvaru

 

                                                                                          (2.1)

 

Zde  je vektor zobecněných výchylek,  vektor buzení a  vektor všech ostatních sil působících na mechanickou soustavu. Všechny vektory jsou dimenze m. Předpokádejme, že lze vektory  dekomponovat na lineární a nelineární část, totiž na

 

                                                                                                     (2.2)

 

kde

 

                                                                                       (2.3)

 

Potom můžeme systém pohybových rovnic (2.1) přepsat do tvaru

 

                                                                            (2.4)

 

kde , a kde  je vektor libovolných silových účinků, které nelze zahrnout do linearizované levé strany rovnice (2.4), a M,B,K jsou konstantní reálné čtvercové matice hmotnosti, koeficientů útlumu a tuhostí, všechny řádu m, kde m je počet stupňů volnosti. Při tom může vzniknout řada speciálních případů, které postupně probereme. Z rovnice (2.4) vyplývá, že řešení se hledá pro linearizovaný systém s korekcí nelinearity (závislé na řešení) v buzení, kde vystupuje jako aditivní šum.

 

2.1 Lineární systémy

Vyznačují se nulovou nelinearitou, tj. , v rovnici (2.4). Pro řešení je účelné převést systém m diferenciálních rovnic 2. řádu na systém 2m rovnic 1. řádu. Označíme-li

 

,

 

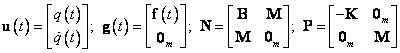dostaneme rozšířením pohybové rovnice o identitu  rovnici

 

                                                                                                          (2.5)

 

Pronásobíme-li tuto rovnici maticí

 

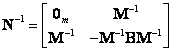                                                                                       (2.6)

 

dostanem systém tzv. stavových rovnic

 

                                                                                                  (2.7)

 

kde

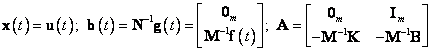          (2.8)

           

a kde  je jednotková matice řádu m.

 

2.2 Volné kmitání

 

Nepůsobí-li na soustavu žádné buzení, je  a systému stavových rovnic vyhovuje řešení . Po dosazení do rovnice (2.7) se dostane obyčejný problém vlastních čísel ve tvaru systému homogenních algebraických rovnic.

 

                                                                                         (2.9)

 

K tomuto problému existuje ještě problém přidružený

 

                                                                                                  (2.10)

 

Řešení x resp. y existují netriviální jen pro určité hodnoty parametru s, které nazýváme vlastními hodnotami. Jsou to ty hodnoty s_k, pro něž . Každé vlastní hodnotě s_k přísluší jeden (pravostranný) vlastní vektor – sloupec x_k a jeden (levostranný) vlastní vektor – sloupec y_k. Vlastní hodnota s_k, společná oběma problémům, souvisí se zobecněnou vlastní frekvencí soustavy Ω_k prostřednictvím vztahu , kde i je imaginární jednička. Vlastní vektory, obecně komplexní, odpovídají vlastním tvarům kmitání. Je-li studovaný systém jednoduché struktury, pak každému vlastnímu číslu přísluší jeden nezávislý vlastní vektor.

První model problému vlastní hodnoty, vyplývající z rovnice (2.7), lze definovat rozšířenými zápisy rovnic (2.9) a (2.10) pro všechny vlastní čísla ve tvaru

 

                                                                               (2.11)

 

kde  je spektrální matice a a  jsou tzv. modální matice vytvořené ze všech k = 1,2 ...., m vlastních vektorů – tvarů kmitů. Vlastní vektory nejsou obecně definovány jednoznačně. Protože by se mohly navzájem lišit v měřítku, kladou se na ně ještě podmínky ortogonality a normy, tj. ortonormality

 

                                                                     (2.12)

Druhý model je definován homogenní variantou rov. (2.5) vedoucí pro  k zobecněnému problému vlastních čísel

 

                                                                           (2.13)

 

s podmínkami normy a ortogonality ve tvaru

 

                                                                                          (2.14)

 

kde opět U a T jsou modálními maticemi, které v případě, že  se rovnají X resp. Y. U obou těchto modelů se pracovalo s maticemi řádu 2m, které však musí obsahovat redundantní informace, neboť obsahují celkem 2.(2m)² prvků, zatímco původní model pouze 3m² prvků v maticích M, B, K. Proto lze dokázat, že platí

 

                        ,                                                                      (2.15)

 

Na tomto základě lze postavit i třetí model problému vlastních čísel, tentokrát však kvadratický v s. Pro jeho řešení se vyjde z homogenní úlohy odpovídající problému (2.4) a dostane se pravostranná a levostranná varianta problému vlastní hodnoty ve tvarech

 

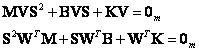                                                                    (2.16)

 

s novými podmínkami normy a ortonormality, které již nejsou tak průhledné

 

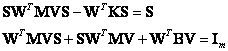                                                                         (2.17)

 

Řešení třetího modelu problému vlastních čísel přímou cestou není dobře možné, protože se jedná o maticový kvadratický problém. K řešení lze využít druhého modelu tak, že ze známých matic M, B a K se sestaví matice N a P a vyřeší se matice S a U. Levostranné vektory v matici T se podle formule 2.14 vypočtou inversí matice [NU]. Z modálních matic T a U se pak odseknou dolní poloviny a po normalizaci zůstanou modální matice V a W typu (m, 2m). Ty se oměřítkují např. tak, aby sobě si odpovídající vlastní vektory měly stejné Čebyševovy normy.

 

2.3 Vynucené kmitání

Vynucené kmity diskrétní lineární mechanické soustavy jsou popsány modelem

 

                                                                    (2.18)

 

V závislosti na tvaru pravé strany je účelné řešit numerickou úlohu různými postupy. Ustálené harmonické kmity lze vyšetřovat poměrně snadno. Je-li pravá strana harmonickou funkcí času  s libovolným komplexním vektorem amplitud f, má ustálené kmitání podobný tvar, totiž . Po dosazení do diferenciální rovnice dostaneme pro frekvenčně závislou komplexní amplitudu ustálené odezvy funkci

 

                               (2.19)

 

Matice  je maticí komplexních dynamických poddajností. Říká se jí rovněž matice frekvenčních přenosů nebo také frekvenčních odezev. Pro každou z budících frekvencí ω existuje jedna komplexní matice  řádu m.

Obecný vynucený kmit lineární soustavy se získá poněkud složitějším postupem. Existují principiálně dva různé způsoby, jak vypočítat odezvu lineárního dynamického systému na obecné vnější buzení: přímá integrace a konvoluce impulstní odezvy s buzením. První přístup, použitelný obecně i pro nelineární systémy, popíšeme až později. Druhý přístup, založený na integrálních transformacích, využívá skutečnosti, že odezva lineárního systému  na buzení  je dána konvolučním integrálem

 

                                                      (2.20)

 

Pokud všechny funkce vstupující do integrálu jsou absolutně integrabilní, lze na rovnici (2.20) aplikovat Fourierovu transformaci (FT) a dostat tak známý tvar obrazu konvoluce jakou součinu obrazů funkcí vstupujících do konvolute

 

                                                                                                  (2.21)

 

Zpětnou FT  se získá odezva . Při numerické realizaci celého postupu pomocí konečné diskrétní FT (její rychlé verze FFT), je zapotřebí pracovat s časovými řadami  a  doplněnými o stejně dlouhé nulové úseky. Za těchto okolností není výsledek zatížen cyklickou chybou vznikající v důsledku diskretizace.

Za jistých předpokladů lze hledat řešení vynuceného kmitání diskrétních lineárních systémů analyticky s použitím maticové exponenciály.

 

2.4 Stabilita

Z polohy vlastních čísel v komplexní rovině lze usuzovat i na chování dynamického systému. Rozviňme vztah popisující volné kmity v čase

 

                                                                                   (2.22)

 

Zde x je vektor komplexních amplitud (vlastních tvarů kmitů),  je člen vyjadřující proměnnost těchto amplitud v čase a

 

                                                                   (2.23)

 

je stacionární kmitavý člen. Je tedy zřejmé, že vlastní kmity budou omezené, pokud reálná část libovolného vlastního čísla bude nekladná. Může nastat pět případů polohy vlastního čísla v komplexní rovině (viz tabulku 2.1 a obrázek 2.1)

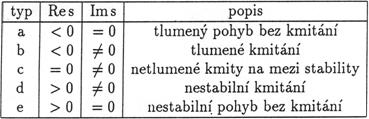
Tabulka 2.1: Přehled typů vlastních čísel

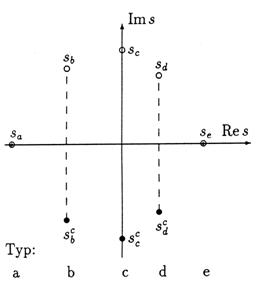
Obr. 2.1: Rozmístění vlastních čísel v Gaussově rovině určuje chování dynamického systému.

 

Pohyby systémů s  (v levé polorovině) jsou stabilní. Vlastní čísla typů b, c, d se vždy vyskytují v komplexně sdružených párech, pokud matice M, B, K jsou reálné. Pro kmitavý systém s jedním stupněm volnosti lze relativní útlum k-tého vlastního čísla stanovit z formule

 

                                                                                                   (2.24)

 

Pro systémy s více stupni volnosti platí tento vztah jen přibližně.

Pro vlastní čísla v levé polorovině budou kmity příslušné frekvence zanikat, kdežto v pravé polorovině budou růst. Pro vlastní čísla na imaginární ose se systém bude chovat jako netlumený. Mechanické diskrétní systémy vytvářené z hmotností, pružin a tlumičů mají matice M a K symetrické a matici B hermitovskou, tj. v reálné části symetrickou a v imaginární antisymetrickou s nulovou diagonálou. U takových systémů se pak setkáváme pouze s vlastními čísly typu a, b, c, tedy bez nestabilit. Připojí-li se však k těmto systémům další účinky, obvykle nevratného charakteru, jako jsou vlivy proudícího média, řezného procesu při obrábění, styku kola s kolejnicí anebo řízení, porušující symetrii původních matic, mohou se vyskytnout i případy typu d, e.

Vlivy porušující symetrii se obvykle mění s některým provozním parametrem (rychlostí proudění, jízdy, řezného procesu, tlakem, teplotou ap.). V souvislosti s tím se mění i poloha vlastních čísel v Gaussově rovině a vlastní číslo původně typu b může pro určitý provoz přejít na typ c až dokonce do režimu d. Tehdy energie odebíraná z pohonu stroje je přes nesymetrické členy matic přiváděna do kmitajícího systému a v okamžiku, kdy se právě rovná energii odváděné tlumícími elementy, nastane stav na mezi stability. Po překročení meze stability přebytek přivedené energie buď rozkmitává lineární soustavu nade všechny meze, nebo ji přivede ke zhroucení (u typu e). Systémy, jejichž vlastní hodnoty se v průběhu změn provozních parametrů mění, se nazývají evolutivními.

© Ústav mechaniky těles, mechatroniky a biomechaniky
Admin e-mail: krejci.p@fme.vutbr.cz

Poslední aktualizace