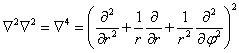Počítačové metody mechaniky v dynamice
Počítačové metody mechaniky v dynamice
1. Problém vlastních hodnot
V podstatě se rozlišují dva druhy problémů vlastních hodnot
· Standardní
· Zobecněný
Standardní
Vychází se ze soustavy algebraických rovnic ve tvaru
![]()
Hledají se vlastní čísla
matice ![]() ,
tak aby platilo
,
tak aby platilo ![]()
Příklad
Stanovte vlastní čísla
matice ![]()
![]()
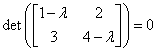
![]()
![]()
![]()
Po zpětném dosazení do
soustavy algebraických rovnic nelze explicitně vypočítat ![]() , protože obě rovnice
jsou lineárně závislé. Tedy např. pro první vlastní číslo
, protože obě rovnice
jsou lineárně závislé. Tedy např. pro první vlastní číslo
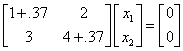
Obvykle se některá z neznámých volí a ostatní se dopočítávají.
Zobecněný
Vychází se z pohybové rovnice pro volné netlumené kmitání (volné kmitání)
![]()
Předpokládané řešení
![]()
a po dosazení
![]()
Zobecnění je dáno tím, že
místo jednotkové matice je matice hmotnosti. Převedení na standardní se provede
vynásobením ![]()
![]()
Nutnou a postačující
podmínkou pro to, aby soustava rovnic měla nenulové netriviální řešení je, aby
determinant matice soustavy byl roven nule. Determinant ![]() se nazývá frekvenční
determinant. Vlastní hodnoty jsou pro úlohy dynamiky vlastní
frekvence kmitání dynamického systému (frekvenční
spektrum). Neznámé v tomto případě
představují pravostranné vlastní vektory (kmitna).
Po uspořádání se obdrží modální matice pravostranných vektorů -
se nazývá frekvenční
determinant. Vlastní hodnoty jsou pro úlohy dynamiky vlastní
frekvence kmitání dynamického systému (frekvenční
spektrum). Neznámé v tomto případě
představují pravostranné vlastní vektory (kmitna).
Po uspořádání se obdrží modální matice pravostranných vektorů - ![]() . Obdobně
bychom mohli stanovit levostranné vektory.
. Obdobně
bychom mohli stanovit levostranné vektory.
Levostranné vektory - ![]()
![]()
Po transponování této rovnice
![]()
Odkud se stanoví
levostranné vlastní vektory. Vlastní čísla jsou stejné. V případě, že
platí ![]() jsou
levostranné a pravostranné vektory stejné
jsou
levostranné a pravostranné vektory stejné
Normování
· Vzhledem k jedničce
· Vzhledem k matici hmotnosti
![]()
![]() kde
kde ![]() je spektrální
matice
je spektrální
matice
Podmínky ortogonality
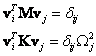
Podmínky ortoganility (kolmosti) vyjadřují nezávislost vlastních tvarů na sobě. Tato skutečnost má dva důsledky:
1. Při harmonickém buzení frekvencí rovné vlastní kmitá soustava pouze jediným tvarem kmitu s frekvencí rovnou budící frekvenci.
2. V případě, že je znám určitý tvar kmitání, nelze na základě této znalosti usuzovat jak budou vypadat (případně je odvodit) ostatní tvary kmitání.
Stavový prostor
V podstatě je to snížení řádu pohybové rovnice
![]()
![]()
Maticový zápis
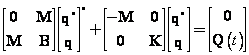
Zkráceně (pro volné kmitání v homogenním tvaru)
![]()
Horní podtržítka značí tzv. rozšířené veličiny. Předpokládané řešení
![]() ,
,
![]() . reálná část
komplexní ho vlastního čísla představuje
tlumení a imaginární část vlastní frekvenci tlumeného
kmitání.
. reálná část
komplexní ho vlastního čísla představuje
tlumení a imaginární část vlastní frekvenci tlumeného
kmitání.
Metody stanovení vlastních čísel a vektorů
· Frekvenční determinant
· Lancoszova metoda
· Metody založené na podobnostní transformaci
|
Metoda |
Typ matice |
Poznámka |
|
Jacobi |
symetrická |
úplný problém |
|
LR algoritmus |
nesymetrická |
úplný problém |
|
QR algoritmus |
nesymetrická |
úplný problém |
|
QZ algoritmus |
nesymetrická |
úplný problém |
|
Lanczosova |
nesymetrická |
částečný |
|
Mocninová |
nesymetrická |
částečný |
|
Housenholderova |
nesymetrická |
částečný |
Důležité veličiny
![]() - vlastní číslo je
komplexně sdružené
- vlastní číslo je
komplexně sdružené
![]() -
vlastní frekvence netlumeného kmitání
-
vlastní frekvence netlumeného kmitání
![]() -
vlastní frekvence tlumeného kmitání
-
vlastní frekvence tlumeného kmitání
![]() - součinitel doznívání,
b – součinitel tlumení
- součinitel doznívání,
b – součinitel tlumení
kritický
útlum ![]() -
-
![]()
![]() -
poměrný útlum
-
poměrný útlum
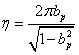 -
logaritmický dekrement útlumu
-
logaritmický dekrement útlumu
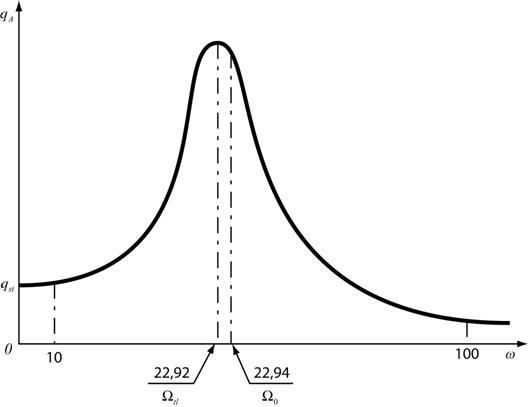
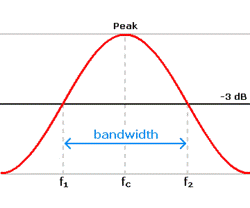
Stanovení
tlumení z amplitudové charakteristiky. Šířka je
stanovena pro amplitudu ![]() nebo při poklesu o 3 dB
nebo při poklesu o 3 dB
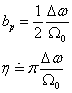
Q -
faktor ![]()
Pokles o 3 dB odpovídá
hodnotě 70.7 %, nebo také hodnotě ![]() (nominální šířka
pásma).
(nominální šířka
pásma).
![]()
![]()
V případě že se vlastní frekvence netlumeného málo liší od vlastní frekvence tlumeného systému, lze přibližně pro stanovení poměrného útlumu (Q faktoru) použít vlastní frekvenci tlumeného systému.
Vlastní hodnoty jsou obecně komplexně sdružená čísla. Reálná část odpovídá tlumení a imaginární je vlastní frekvence kmitání. Reálná část rozhoduje o stabilitě dynamického systému. Kladná znamená nestabilní a záporná stabilní. Vlastní čísla lze zobrazit v Gausově rovině. Každému vlastnímu číslu odpovídá i určitý tvar odezvy v časové oblasti.
Rayleighův kvocient
Využívá se pro přibližné stanovení zpravidla nejnižší vlastní frekvence. Patří mezi přibližné metody řešení dynamických vlastností kontinuí.
![]()
Pro r-tou (zpravidla nejnižší) vlastní frekvenci pak je
![]()
odtud
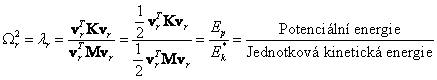
Ritzova metoda
Podstata metody: Rayleighův kvocient leží v intervalu přesných hodnot vlastních úhlových rychlostí. Proto se vlastní tvar aproximuje lineární kombinací nezávislých funkcí, které splňují OP. Vlastní tvar minimalizuje Rayleighův kvocient. Např. pro jednorozměrné kontinuum
![]()
Pak
![]()
a musí být
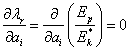
![]()
![]() pro
pro ![]()
Obdrží se soustava n homogenních algebraických rovnic. Pro jeden konečný prvek není mezi Ritzovou metodou a MKP žádný rozdíl.
2. Metody redukce
V podstatě je to snížení řádu úloh (snížení počtu stupňů volnosti). Metody:
1. Přímá
2. Fyzikální
3. Guyanova
4. Modální
5. Ve frekvenční oblasti
2.1 Přímá redukce
Je to přímé vynechání řádků a sloupců.
2.2 Fyzikální redukce
Někdy se této metodě říká metoda přetvořením mechanického modelu. V podstatě se používají dva druhy. Dva pružné členy se redukují na jeden a druhý, kdy se dva setrvačné členy redukují na jeden.
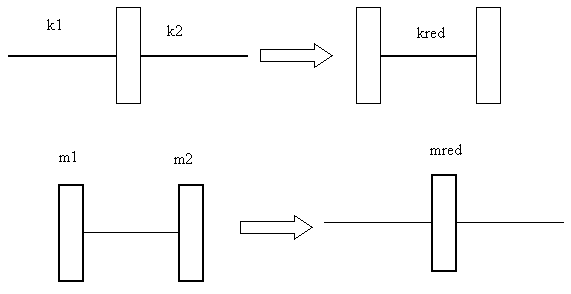
Příklady redukce
2.3 Guyanova redukce
Někdy je tato metoda nazývána jako statická kondenzace. Podstata spočívá v rozdělení matice tuhosti na hlavní (m - master) a vedlejší (s - slave) prvky, přičemž vedlejší nesmí být zatíženy.
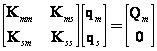
![]()
Po dosazení za ![]() z druhé
rovnice do první je
z druhé
rovnice do první je
![]()
pak
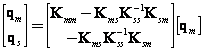
Transformační matice pak má tvar
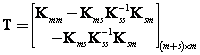
Celá pohybová rovnice
![]()
a dále po násobení transponovanou transformační maticí zleva
![]()
2.4 Modální redukce
Podstatou je transformace
pohybové rovnice z fyzikálních souřadnic do hlavních. Fyzikální souřadnice
![]() mají
rozměr, hlavní
mají
rozměr, hlavní ![]() nemají. Transformační rovnice má tvar
nemají. Transformační rovnice má tvar
![]()
kde ![]() je modální matice
pravostranných vektorů
je modální matice
pravostranných vektorů
Pohybová rovnice ve fyzikálních souřadnicích
![]()
Pohybová rovnice ve fyzikálních souřadnicích
![]()
Po násobení transponovanou modální maticí (obecně) levostranných vlastních vektorů se obdrží
![]()
S přihlédnutím k normě vzhledem k matici hmotnosti se obdrží
![]()
Jeli matice ![]() diagonální
(případ tzv. komutativního tlumení), rozpadá se
soustava n diferenciálních rovnic druhého řádu na n nezávislých
diferenciálních rovnic druhého řádu. V tomto případě lze analyzovat
příspěvek jednotlivých tvarů kmitání na celkové
odezvě. Redukce nyní spočívá v zahrnutí pouze určitého počtu tvarů
kmitání do řešení, tedy
diagonální
(případ tzv. komutativního tlumení), rozpadá se
soustava n diferenciálních rovnic druhého řádu na n nezávislých
diferenciálních rovnic druhého řádu. V tomto případě lze analyzovat
příspěvek jednotlivých tvarů kmitání na celkové
odezvě. Redukce nyní spočívá v zahrnutí pouze určitého počtu tvarů
kmitání do řešení, tedy

je pohybová rovnice řádu ![]() .
.
2.5 Redukce ve frekvenční oblasti
Výchozím vztahem pro redukci ve frekvenční oblasti je vztah pro dynamickou poddajnost (viz níže)
![]()
Do řešení zahrne pouze určitý počet vlastních hodnot a určitý počet souřadnic ve vlastních vektorech. Například v případě zahrnutí pouze druhého a pátého prvku ve vlastních vektorech má čitatel (Dyadický součin) tvar. Přidáním dalšího vlastního čísla (vektoru) se řád matice nemění.
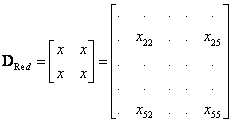
3. Proporcionální tlumení
Velmi častý případ výpočtového modelování tlumení ( viskózní tlumení). Předpoklad:
![]()
Po úpravě
![]()
pro j-tý tvar kmitu
![]()
![]() - hlavní (modální)
tlumení
- hlavní (modální)
tlumení
![]() - hlavní (modální)
hmotnost
- hlavní (modální)
hmotnost
![]() - hlavní (modální)
tuhost
- hlavní (modální)
tuhost
![]()
![]()
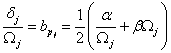
Nebo
![]()
Jak již bylo uvedeno, vlastní frekvenci tlumeného kmitání a součinitel doznívání, resp. poměrný útlum lze stanovit experimentálně. Zde mohou nastat tři základní případy.
1. Případ – znají se
vlastní frekvence a poměrné útlumy od dvou tvarů
kmitání. Koeficienty ![]() a
a ![]() se stanoví ze soustavy dvou
algebraických rovnic
se stanoví ze soustavy dvou
algebraických rovnic
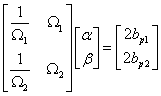
2. Případ – zná se vlastní frekvence a poměrný útlum jenom od jednoho tvaru kmitání. Druhá rovnice se stanoví za předpokladu, že v převážné většině technických aplikací je nejméně tlumen nejnižší tvar kmitání. Tedy z podmínky extrému lze stanovit rovnici
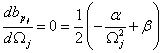
Koeficienty ![]() a
a ![]() se stanoví ze
soustavy dvou algebraických rovnic
se stanoví ze
soustavy dvou algebraických rovnic
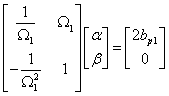
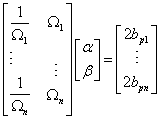
3. Případ – znají se
vlastní frekvence a poměrné útlumy od více jak dvou
tvarů kmitání. Koeficienty ![]() a
a ![]() se stanoví
z přeurčené soustavy algebraických rovnic
se stanoví
z přeurčené soustavy algebraických rovnic
Poznámka:
·
Zpravidla se volí koeficient ![]()
·
Zpravidla se volí koeficient ![]()
·
Koeficientem ![]() se modeluje konstrukční
tlumení
se modeluje konstrukční
tlumení
·
Koeficientem ![]() se modeluje materiálové
tlumení
se modeluje materiálové
tlumení
· Pozor, oba koeficienty mají rozměr
4. Odezva při vynuceném kmitání ( vynucené kmitání)
Pohybová rovnice
![]()
kde ![]() je buzení soustavy (
vnější síla, moment). Řešení se skládá z řešení
homogenní části a partikulárního integrálu, tedy
je buzení soustavy (
vnější síla, moment). Řešení se skládá z řešení
homogenní části a partikulárního integrálu, tedy
![]()
Dva základní případy
· Ustálené kmitání (řešení ve frekvenční oblasti) – partikulární integrál
· Přechodové kmitání (odezva v časové oblasti)
4.1 Odezva při vynuceném ustáleném kmitání
Pohybová rovnice za předpokladu harmonického buzení má tvar ( amplituda buzení je komplexní)
![]()
kde ![]() je amplituda budících
účinků (vnější síla, moment)
je amplituda budících
účinků (vnější síla, moment)
Řešení se předpokládá ve tvaru
![]()
Po dosazení
![]()
dynamická tuhost (přímá dynamická tuhost, fázově posunutá dynamická tuhost)
![]()
Dynamická poddajnost
![]()
Obdobně při řešení ve stavovém prostoru
![]()
Dynamická poddajnost má v tomto případě tvar (vynechán horní pruh)
![]()
Dynamickou poddajnost lze rovněž stanovit na základě modální transformace. V tomto případě je
![]()
Poznámka: v čitateli je tzv. dyadický součin.
Pak odezvu při vynuceném ustáleném kmitání lze stanovit ze vztahů
Bez redukce
![]()
Při využití Guanovy redukce
![]()
Při využití modální redukce (transformace)
![]()
![]()
Při využití redukce ve frekvenční oblasti
![]()
Pro 1 st. volnosti
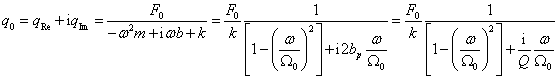
komplexní funkce frekvenční odezvy (přenosová funkce při aplikaci Laplaceovy transformace)
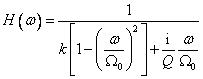
Modul a fáze
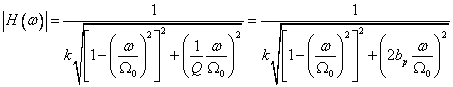
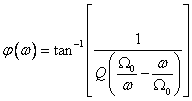
Poznámka
Stav kdy je frekvence buzení rovna vlastní (tlumeného i netlumeného kmitání) se nazývá rezonance (opak antitrezonance).
Metoda trigonometrických kolokací
Tato metoda kombinuje řešení
odezvy při vynuceném ustáleném kmitání
s řešením v časové oblasti. Jedná se o poměrně novou metodu. Buzení
soustavy lze vyjádřit buď v reálném, nebo komplexní
m oboru. V této kapitole bude celá analýza provedena v reálném oboru.
Předpokládejme, že buzení je periodické se známými násobky
budící frekvence, které
lze zapsat jako prvky množiny ![]() s prvky
s prvky ![]() ve tvaru
ve tvaru
![]() kde
kde ![]() .
.
Předpokládejme, že i odezva je
periodická s předpokládanými násobky budící
frekvence, které lze zapsat jako prvky množiny ![]() s prvky
s prvky ![]() ve tvaru
ve tvaru
![]() kde
kde ![]() .
.
budící sílu při zahrnutí statického zatížení tak lze obecně vyjádřit ve tvaru
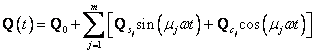
kde indexy ![]() značí sinovou a
kosinovou složku. Řešení pohybové rovnice předpokládejme ve stejném tvaru
značí sinovou a
kosinovou složku. Řešení pohybové rovnice předpokládejme ve stejném tvaru
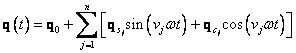
Volba počtu a typu násobků závisí na typu nelinearity vazebného elementu. Obecně nelineární pohybová rovnice s ohledem na aplikaci metody trigonometrické kolokace v rotorových soustavách má tvar
![]()
Pro rychlost a zrychlení platí

Po dosazení a porovnáním členů u stejných neznámých se po úpravě obdrží
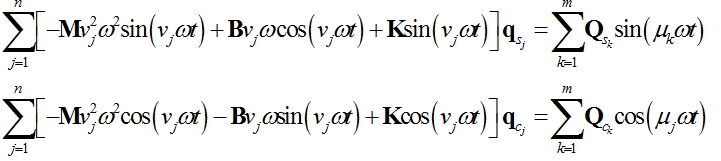
Označení pro
kolokační čas ![]()
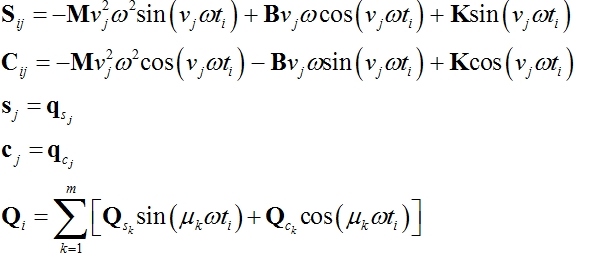
Zkráceně pak
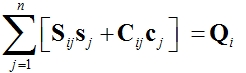
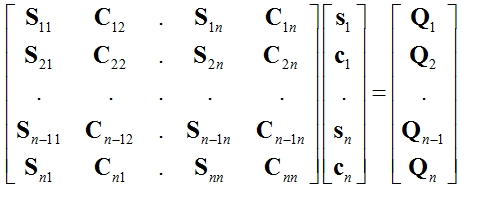
Goniometrické funkce v rovnicích jsou pro daný čas a násobek konstanty. Konkrétní časové okamžiky se stanoví rozdělením nejmenší periody v požadovaném spektru odezvy na konečný počet hodnot. Pak má pohybová rovnice má tvar
4.2 Odezva při přechodovém kmitání
Je to řešení v časové oblasti. Fourierovou transformací ( rychlá Fourierova transformace) lze získat řešení ve frekvenční oblasti.
Pohybová rovnice
![]()
kde ![]() je buzení soustavy (
vnější síla, moment)
je buzení soustavy (
vnější síla, moment)
počáteční
podmínky pro ![]() pohybu hřídele jsou dány vztahy
pohybu hřídele jsou dány vztahy
![]() .
.
Odezva při přechodovém kmitání
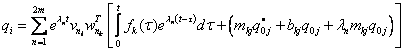
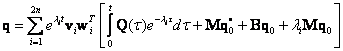
Na základě modální transformace
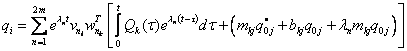
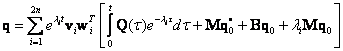
Na základě Laplaceovy transformace
Pohybová rovnice
![]()
dále je ![]() - parametr
Laplaceovy transformace
- parametr
Laplaceovy transformace
![]() - matice
dynamických tuhostí
- matice
dynamických tuhostí
![]() - matice dynamických
poddajností
- matice dynamických
poddajností
![]()
![]()
![]() - z toho
se určí vlastní čísla
- z toho
se určí vlastní čísla ![]()
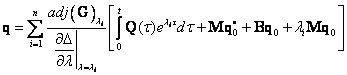
kde pro 1 st. volnosti
![]()
kde ![]() je tzv. Duhamelův
integrál
je tzv. Duhamelův
integrál
Metody přímé integrace pohybových rovnic
V podstatě se metody dělí na explicitní a implicitní.
Metody: - explicitní
(Diferenční, R-K) - ![]()
![]() (kinematika)
(kinematika)
-
implicitní (Newmarkova, R-K) -![]()
Metody Runge-Kuttovy (R-K)
Druhy:
- explicitní
- implicitní
Řešení diferenciální rovnice ( stavový prostor)
![]()
odkud
![]()
Podstata metod
![]()
kde ![]() - jsou konstanty
- jsou konstanty
![]() - funkční hodnoty
- funkční hodnoty
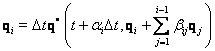
Metoda druhého řádu
![]()
Metoda třetího řádu
![]()
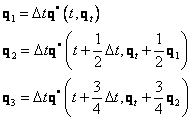
Metoda čtvrtého řádu
![]()
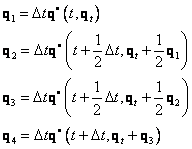
Metoda centrálních diferencí
![]()
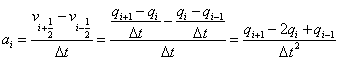
Newmarkova metoda
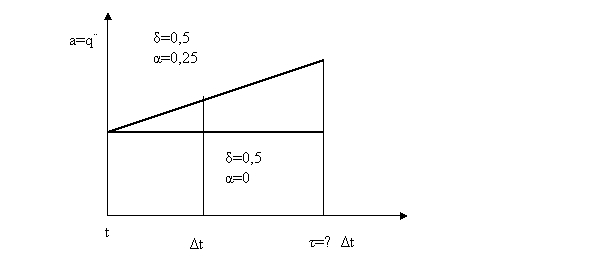
![]()
![]()
![]()
![]()
![]()
![]()
![]()
5. Kmitání kontinua
Zde budou analyzovány pouze některé základní typy kontinua ( spojitý model).
Poznámka: srovnání s tuhým tělesem (tuhé těleso)
1. Podélné kmitání prutů
2. Torzní kmitání prutů
3. Příčné kmitání prutů
4. Kmitání membrán
5. Kmitání desek
Základní vztahy pro sestavení výchozí rovnice pro analýzu dynamických vlastností
1. Rovnice rovnováhy (pohybová), zatížení zde představuje spojitě rozložené zatížení.
2. Konstitutivní vztahy (Hookeův zákon)
3. Rovnice kompatibility (spojitosti)
5.1 Podélné kmitání prutů
1. Newtonův přístup
1. Rovnice rovnováhy (pohybová)
![]()
![]()
![]()
kde ![]() je
axiální síla (síla)
je
axiální síla (síla)
2. Konstitutivní vztahy (Hookeův zákon)
![]() kde
kde ![]() je
axiální napětí
je
axiální napětí
3. Rovnice kompatibility (spojitosti)
![]()
Shrnutí
![]()
![]()
Potom
![]()
Řešení (zavedení substituce)
![]()
Analýza volného netlumeného kmitání (modální vlastnosti)
![]()
Po dosazení do pohybové rovnice
![]()
![]()
Řešení
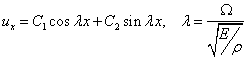
Příklad: oboustranně
vetknutá tyč: ![]()
![]()
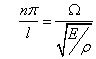
![]()
2. Přístup na základě MKP
Princip virtuálních prací – obecně
![]()
![]()
MKP:
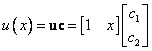
![]()
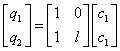
odkud pro setrvačné síly
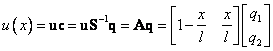
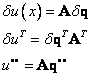
pro elastické (vnitřní síly)
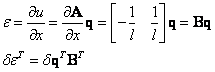
Hookeův zákon
![]()
![]()
Výsledný vztah
![]()
![]()
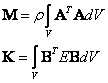
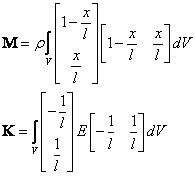

5.2 Torzní kmitání
Newtonův přístup
1. Rovnice rovnováhy (pohybová)
![]()
kde M je
kroutící moment, ![]() je úhlové
natočení, (druhá derivace podle času je úhlové
zrychlení)
je úhlové
natočení, (druhá derivace podle času je úhlové
zrychlení)
2. Konstitutivní vztahy (Hookeův zákon)
![]()
3. Rovnice kompatibility (spojitosti)
![]()
Shrnutí
![]()
Potom
![]()
Řešení
![]()
Analýza volného netlumeného kmitání (modální vlastnosti)
![]()
Po dosazení do pohybové rovnice
![]()
![]()
Řešení
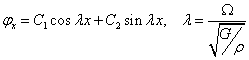
Příklad: oboustranně vetknutá tyč:
![]()
![]()
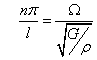
![]()
5.3 Příčné kmitání prutů ( ohybové)
Newtonův přístup
Výsledná rovnice pro příčné (volné netlumené) kmitání prutů
![]()
Řešení
![]()
Analýza volného netlumeného kmitání (modální vlastnosti)
![]()
Po dosazení do pohybové rovnice
![]()
![]()
![]() ,
,
kde
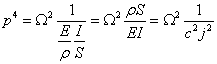
a dále
![]()
Obecné řešení lze vyjádřit
několika způsoby, přičemž nejvýhodnější je ve tvaru tzv. Rayleighových,
(Krylovových) funkcí), kde ![]() je průhyb
nosníku
je průhyb
nosníku
![]()
kde

Výhoda např.
![]() ,
, ![]() atd.
atd.
a navíc respektují OP
Typy OP: ![]()
Příklad OP jednostranně vetknutého prutu (vetknutý nosník)
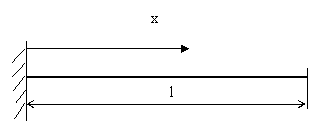
Pro x = 0, ![]()
Pro x = l, ![]()
Poznámka: obdobně pro ostatní okrajové podmínky, případně jejich kombinace (rotační vazba, resp. obecná). Vyšší tvary kmitání mají po délce uzly (uzel).
5.4 Kmitání membrán
Membrány nepřenášejí ohybové momenty.
Druhy:
- kruhové
- obdélníkové
Řešení:
- v kartézských souřadnicích - obdélníkové
- v polárních souřadnicích - kruhové
Pohybová rovnice
![]()
![]()
Obdélníková membrána
Laplaceův operátor
![]() ,
,
Obecné řešení (pro průhyb) tvar
![]()
![]()
![]()
OP + tvary kmitání
ve směru x : 2
ve směru y : 2
Kruhová membrána
Obecné řešení má tvar (pro průhyb)
![]()
a pak dále
![]()
![]()
OP + tvary kmitání
5.5 Kmitání desek
Desky přenášejí ohybové momenty.
Druhy:
- kruhové
- obdélníkové
Řešení:
- v kartézských souřadnicích - obdélníkové
- v polárních souřadnicích - kruhové
Pohybová rovnice
![]()
Obdélníková deska
![]()
kde
![]()
Obecné řešení (pro průhyb) má tvar
![]()
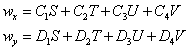
OP + tvary kmitání
ve směru x : 4
ve směru y : 4
Příklad: Stanovte okrajové podmínky pro obdélníkovou desku na jednom okraji vetknutou a na druhém podepřenou
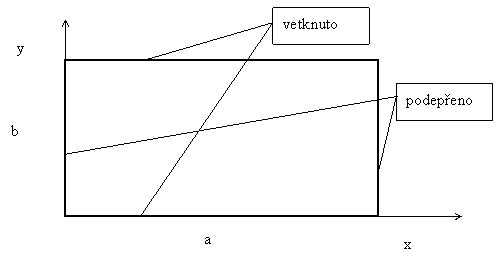
Pro x = 0, ![]() ,
, ![]()
Pro x = a, ![]() ,
, ![]()
Pro y = 0, ![]() ,
, ![]()
Pro y = b, ![]() ,
, ![]()
Kruhová deska
Laplaceův operátor
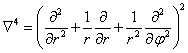
Obecné řešení má tvar
![]()
Řešení v obvodovém směru
![]()
Řešení v radiálním směru
![]()
OP + tvary kmitání (analogie s příčným kmitání prutů)
v radiálním směru: 4
Příklad 1
Stanovte okrajové podmínky pro desku s otvorem na vnitřním poloměru volnou a na vnějším vetknutou
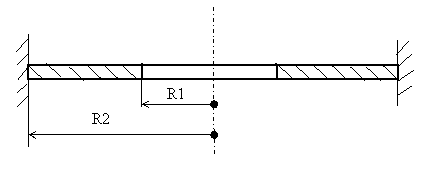
Pro ![]()
Pro ![]()
Příklad 2
Stanovte okrajové podmínky pro desku bez otvoru a na vnějším podepřenou
Pro ![]()
Pro ![]()
Poznámka:
Řešení dynamických vlastností kmitání membrán a desek zpravidla vede na řešení řadami, tedy Besselovými funkcemi. Besselovy funkce jsou různých druhů. Besselovy funkce jsou řešením Besselovy diferenciální rovnice řádu N:
![]()
Besselovy funkce (viz Matlab) jsou:
BESSELJ(N,Z) Besselovy funkce prvního druhu, řádu N
BESSELY(N,Z) Besselovy funkce druhého druhu řádu N
BESSELI(N,Z) Modifikované Besselovy funkce prvního druhu řádu N
BESSELK(N,Z) Modifikované Besselovy funkce druhého druhu řádu N
BESSELH(N,K,Z) Hankelova funkce řádu N
AIRY(K,Z) Airyho funkce
Shrnutí
|
|
Membrána |
Deska |
|
Obdélníková |
Obecné řešení
|
Obecné řešení
|
|
Kruhová |
Obecné řešení
a dále
|
Obecné řešení
a dále
|
Tvary kmitu:
· uzlové čáry (obdélníkové)
· uzlové plochy (obdélníkové)
· uzlové průměry (kruhové)
· uzlové kružnice (kruhové)
6. Metoda přenosových matic
V nedávné době velmi používaná metoda pro řešení kmitání řady konstrukcí. Je nenáročná na paměť počítače.
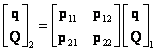
![]()
![]()
![]()
![]()
Poznámky
-
matici ![]() je neznámá frekvence
je neznámá frekvence
- zahrnutí OP
- výpočet vlastních vektorů
- řešení vynuceného ustáleného kmitání
- řešení přechodového kmitání
- možná kombinace MKP a MPP
Příklad
Sestavení rovnice pro analýzu dynamických vlastností volného netlumeného kmitání dynamického řetězce na jedné straně vetknutého a na druhé straně volného.
Úplně uvolněné i-té těleso je na obrázku. Uzly jsou označeny písmeny 1 a 2.

Pohybová rovnice z pohledu MKP má tvar
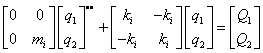
Předpokládané řešení pro případ harmonického buzení a kmitání
![]()
Po dosazení
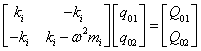
Po převedení do tvaru vhodného pro metodu přenosových matic
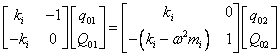
Výsledná rovnice pro konečný prvek má tvar
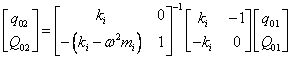
a matice přenosu
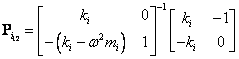
Přenos mezi místem 1 a n se stanoví násobením lokálních přenosových matic. Po zahrnutí okrajových podmínek má výsledná rovnice tvar
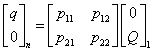
Z druhé rovnice potom je
![]()
Nutnou a postačující podmínkou pro to, aby soustava rovnic měla nenulové netriviální řešení je, aby determinant matice soustavy byl roven nule, tedy
![]()
V obecnějším případě
je submatice ![]() funkcí frekvence.
frekvence pro níž je determinant roven nule je
vlastní frekvence volného netlumeného
kmitání otevřeného řetězce. Zpětným dosazením
vlastních frekvencí do rovnic pro přenos mezi jednotlivými uzly se pro jednu
zvolenou veličinu (matice je singulární) vypočítají vlastní vektory.
funkcí frekvence.
frekvence pro níž je determinant roven nule je
vlastní frekvence volného netlumeného
kmitání otevřeného řetězce. Zpětným dosazením
vlastních frekvencí do rovnic pro přenos mezi jednotlivými uzly se pro jednu
zvolenou veličinu (matice je singulární) vypočítají vlastní vektory.
Metoda konečných prvků
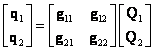 (silová varianta – neznámé jsou
síly)
(silová varianta – neznámé jsou
síly)
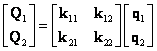 (deformační varianta – neznámé
jsou deformace)
(deformační varianta – neznámé
jsou deformace)
7. Citlivostní analýza
V podstatě chceme stanovit, na změnu kterého parametru jsou nejvíce citlivé modální vlastnosti dynamického systému. Chceme tedy stanovit:
![]()
Postup – pouze pro ![]()
![]()
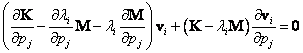
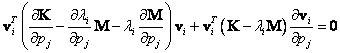
![]()
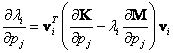
Výsledkem pak je matice
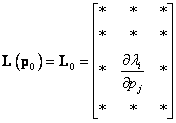
8. Ladění mechanických soustav
![]()
Vektor naladění
![]()
Vektor parametrů
![]()
Vektor požadovaných modálních veličin
![]()
Vektor vybraných neznámých (vypočítaných) parametrů
![]()
Matematická formulace ladění
![]()
Metoda postupných lineárních aproximací
Taylorův rozvoj
![]()
Jacobiho matice zobrazení (matice ladění, nebo matice citlivosti)
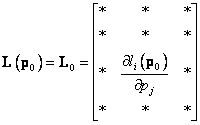
![]()
maticově
![]()
zkráceně
![]()
odtud s ohledem na výsledné řešení je
![]()
Postup ladění
![]() známe
známe
1. Určení
všech modálních vlastností – ![]()
2. Výběr
požadovaných modálních vlastností – ![]()
3. Citlivostní analýza – kompletní
4. Výběr
parametrů pro ladění - ![]() pro největší spády
pro největší spády
5. Volba chyby
6. Rozhodnutí o zavedení přípustné oblasti
7. Proces ladění - iterace
9. Metody řešení nelineárního kmitání
Metody. Přímá linearizace
Ekvivalentní linearizace
Taylorův rozvoj
Přímá linearizace
![]()
![]()
![]()
Ekvivalentní linearizace
Předpoklad: harmonické buzení
harmonické kmitání
![]()
![]()
![]()
a dále
![]()
Podstata – rozvoj funkce ![]() ve Fourierovu
řadu
ve Fourierovu
řadu
![]()
kde koeficienty jsou
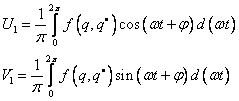
![]()
Taylorův rozvoj
Podstata spočívá v rozvoji nelineární funkce v Taylorovu řadu, přičemž se berou v úvahu pouze její první ( lineární) členy. Předpoklad malých kmitů kolem rovnovážné polohy
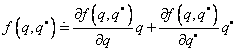
Vlastnosti nelineární ho kmitání:
· subharmonické kmitání
· ultraharmonické kmitání
10. Stabilita pohybu
Stabilitu lze definovat z různých hledisek
· dynamická stabilita
· globální stabilita
· lokální stabilita
· stabilita struktury
· stabilita tvaru
· stabilita ve smyslu Lagrange
· stabilita ve velkém
· stabilita ve smyslu Ljapunova
· technická stabilita
Kritéria posouzení stability
· Na základě reálné části komplexní ho vlastního čísla
· Routhovo – Hurwitzovo kritérium
· Analýza ve fázové rovině
· Ljapunovy exponenty
· Floquetovo kritérium
· Analýza v Gausové rovině
Vlastní číslo ![]() - (
stabilita typu divergence, nebo flutter)
- (
stabilita typu divergence, nebo flutter)
Routhovo - Hurwitzovo kritérium
Ve staticky rovnovážné poloze je rychlost pohybu nulová. Jestliže na soustavu nepůsobí vnější síly, které nemají potenciál, staticky rovnovážná poloha se stanoví (na základě Lagrangeových rovnic II. druhu) z rovnice
![]()
Jednou z možností o rozhodnutí stabilní, či nestabilní rovnovážné polohy je druhá derivace, tedy pro stabilní rovnovážnou polohu misí být
![]()
O tom zda bude staticky rovnovážná poloha stabilní, nebo labilní lze rozhodnout např. na základě Routhova – Hurwitzova kritéria. Nejdříve je nutno sestavit tzv. charakteristickou rovnici
![]()
Nutnou a postačující podmínkou pro to, aby charakteristická rovnice měla všechny kořeny se zápornou reálnou částí je splnění nerovností:
1. ![]()
2. 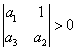 ,
, 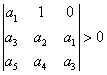 ,
, 
Ljapunova definice stability v tzv. „malém“
Nerozrušený pohyb je
stabilní, jestliže pro každé kladné malé číslo ![]() lze nalézt takové kladné číslo
lze nalézt takové kladné číslo ![]() , že pro
všechny rušivé pohyby pro které platí
, že pro
všechny rušivé pohyby pro které platí ![]() bude pro všechna
bude pro všechna ![]()
![]() . Jestliže takové
. Jestliže takové ![]() neexistuje,
pohyb je nestabilní.
neexistuje,
pohyb je nestabilní.
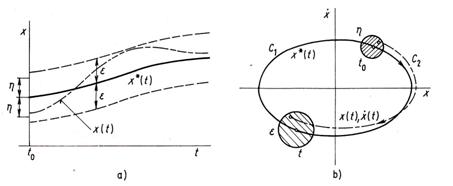
Fázová rovina (Hayashiho)
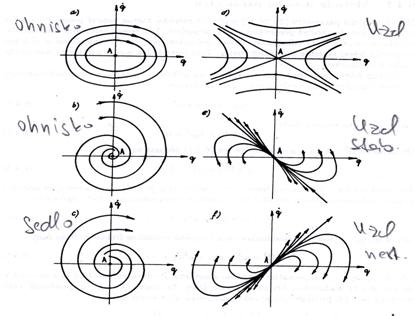
Jestliže se pohyb zastupujícího bodu blíží k ohnisku, dynamický systém je stabilní a pokud se vzdaluje, dynamický systém je nestabilní.
Ljapunovy exponenty
Exponenty polynomu rozhodují o stabilitě dynamického systému. Jejich výpočet je značně časově náročný a provádí se v časové oblasti.
Fluqetovo kritérium (Floquetova věta)
Floquetova teorie se vztahuje k soustavě lineárních obyčejných diferenciálních rovnic prvního řádu
![]()
kde matice A je spojitá periodická funkce s periodou T. Matice F se nazývá maticí fundamentálních řešení, přičemž sloupce jsou lineárně závislými řešeními. Pak lze řešení soustavy rovnic napsat ve tvaru
![]()
Matice
![]()
se nazývá přenosová, nebo
také přechodová matice z času ![]() do času
do času ![]() . Není-li matice
. Není-li matice ![]() funkcí času
(konstantní), pak je matice přenosu dána vztahem
funkcí času
(konstantní), pak je matice přenosu dána vztahem
![]()
což je tzv. maticová
exponenciála. Je-li matice ![]() funkcí času, pak je matice přenosu dána
vztahem
funkcí času, pak je matice přenosu dána
vztahem
![]()
Mezi časy 0 a T (perioda) pak je
![]()
nebo
![]()
(kdy je ![]() ). Matice
). Matice ![]() se nazývá matice
monodromie. Matice
se nazývá matice
monodromie. Matice ![]() je dle Floquetovy věty regulární a
rovnice
je dle Floquetovy věty regulární a
rovnice ![]() představuje
podobnostní transformaci (nemění se vlastní čísla matice před transformací a po
ní). Pak vlastní čísla matice
představuje
podobnostní transformaci (nemění se vlastní čísla matice před transformací a po
ní). Pak vlastní čísla matice ![]() a matice
a matice ![]() jsou stejné. Pak stačí,
posuzovat stabilitu pouze podle matice přenosu
jsou stejné. Pak stačí,
posuzovat stabilitu pouze podle matice přenosu ![]() . Nutnou a postačující podmínkou
pro to, aby dynamický systém byl stabilní je, aby velikost všech vlastních čísel
mezi časy 0 a T ležela v rozsahu 0-1.
. Nutnou a postačující podmínkou
pro to, aby dynamický systém byl stabilní je, aby velikost všech vlastních čísel
mezi časy 0 a T ležela v rozsahu 0-1.
Stanovení matice ![]() (4 přístupy)
(4 přístupy)
Homogenní tvar pohybových rovnic ve stavovém prostoru má tvar (pro zjednodušení zápisu je vynechán horní pruh)
![]()
tento lze upravit na tvar
![]()
nebo také
![]()
Matici přenosu je nejvýhodnější počítat numericky.
1. Přístup
Je-li časový úsek ![]() rozdělen na n
časových kroků, pak
rozdělen na n
časových kroků, pak
![]()
tedy přes maticovou exponenciálu
2. Přístup
Je-li časový úsek ![]() rozdělen na n
časových kroků. Je-li časový krok integrace malý, lze během tohoto kroku
považovat matici A za konstantní a platí
rozdělen na n
časových kroků. Je-li časový krok integrace malý, lze během tohoto kroku
považovat matici A za konstantní a platí
![]()
Při použití explicitní metody je
![]()
odtud
![]()
a matice přenosu mezi sousedními kroky výpočtu
![]()
![]()
3. Přístup
Je-li časový úsek ![]() rozdělen na n
časových kroků. Je-li časový krok integrace malý, lze během tohoto kroku
považovat matici A za konstantní a platí
rozdělen na n
časových kroků. Je-li časový krok integrace malý, lze během tohoto kroku
považovat matici A za konstantní a platí
![]()
Při použití implicitní metody je
![]()
odtud
![]()
a matice přenosu mezi sousedními kroky výpočtu
![]()
![]()
4. Přístup
Přímým výpočtem odezvy v čase T na základě zvolených počátečních podmínek. V podstatě se provádí opakovaně výpočet odezvy v čase T na základě zvolených počátečních podmínek. Tento výpočet se opakuje n krát.
![]()
K výpočtu odezvy v čase T lze využít některou z přímých metod integrace pohybových rovnic.
Poznámka: V případě použití metod přímé integrace pohybových rovnic lze rovněž využít Newmarkovu metodou, případně Runge – Kutha 4. řádu. Explicitní, nebo implicitní metoda zde byla ukázána pouze pro názornost
Analýza v Gausové rovině
Používá se při řešení vynuceného ustáleného kmitání. Pokud je pohyb zastupujícího bodu v Gausové rovině ve smyslu hodinových ručiček, dynamický systém je stabilní a naopak.
11. Dynamický tlumič vibrací
Pro jednoduchost bude ukázán princip dynamického tlumiče vibrací na kmitání soustav s 1 st. volnosti. Amplitudo frekvenční charakteristika má tvar
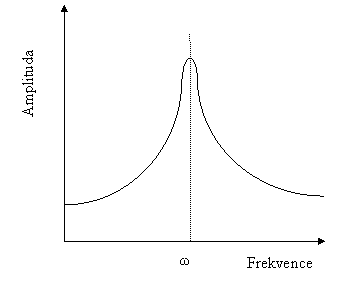
Amplitudová charakteristika původní soustavy
Požadavkem nyní je, aby v rezonanci byla amplituda minimální. Jedním ze způsobů jak toho lze dosáhnout je, přidat k tomuto dynamickému systému druhý. Tím se soustava s 1 st. volnosti změní na soustavu se 2 st. volnosti. Při buzení původní rezonanční frekvencí, těleso první kmitá minimálně avšak kmitá těleso druhé, přídavného tlumiče. Vhodným tlumičem umístěným na druhém tělese (tlumiče) se sníží i kmitání tohoto tělesa a dochází tak ke zmaření energie.
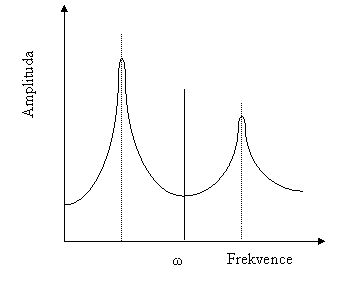
Amplitudová charakteristika nové soustavy
Poznámka: tlumič je funkční pouze při jedné budící frekvenci. V případě polyharmonického buzení je návrh tlumiče obtížnější.
12. Elektro mechanická analogie
Existuje analogie kmitání v mechanice a v elektrotechnice. Schéma mechanické soustavy je všeobecně známa, proto zde není nakreslena.
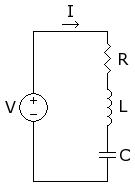
Odpovídající veličiny
|
Mechanika |
Elektrotechnika |
||
|
Hmotnost |
m |
Indukce |
L |
|
Tuhost |
k |
Elektrická elastance |
|
|
Tlumení |
b |
Odpor |
R |
|
Buzení |
Q |
Časová změna napájecího napětí |
|
|
Výchylka |
q |
Proud |
|
|
Rychlost |
v |
Časová změna proudu |
|
|
zrychlení |
a |
Druhá derivace proudu |
|
Pohybové rovnice
![]()
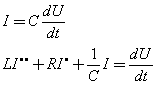
Další veličiny
|
|
Vlastní frekvence |
Součinitel doznívání |
|
Mechanika |
|
|
|
Elektrotechnika |
|
|
13. Příklady
Budou ukázány dva příklady na řešení odezvy při vynuceném ustáleném kmitání. Je to doplnění příkladů, které jsou ve studijních oporách pro dynamiku.
13.1 Příklad 1 – kinematické buzení
Je dána
soustava těles podle obrázku. Základní těleso, ke
kterému je vázán pružný člen koná harmonický pohyb ![]() . Kotouč o
hmotnosti
. Kotouč o
hmotnosti ![]() a poloměru
a poloměru ![]() je pevně spojen s tyčí o
hmotnosti
je pevně spojen s tyčí o
hmotnosti ![]() délky
délky ![]() .
. ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Soustava
se nachází ve staticky rovnovážné poloze a předpokládejte malé kmity kolem této
polohy. Předpokládejte, že dynamický systém je lineární.
. Soustava
se nachází ve staticky rovnovážné poloze a předpokládejte malé kmity kolem této
polohy. Předpokládejte, že dynamický systém je lineární.
Pro danou soustavu řešte:
1. Stanovte vlastní frekvenci netlumeného a tlumeného kmitání a znázorněte amplitudovou charakteristiku.
2. Rozhodněte, zda v pásmu provozního buzení nastane vymezení vůle v.
Rozbor úlohy
Soustava těles představuje soustavu, která má jeden stupeň volnosti. K sestavení pohybové rovnice budou využity Lagrangeovy rovnice druhého druhu. K analýze kmitání lze přistupovat dvěma způsoby.
Schéma prvního
způsobu je na prvním obrázku. Jako zobecněná
souřadnice je zvoleno natočení soustavy, tedy ![]() . Výsledkem bude kontrola
vymezení vůle podle vztahu
. Výsledkem bude kontrola
vymezení vůle podle vztahu ![]() .
.
Schéma druhého
způsobu je na druhém obrázku. Jako zobecněná
souřadnice je zvoleno posunutí koncového bodu na
tyčce, tedy ![]() .
Výsledkem bude kontrola vymezení vůle podle vztahu
.
Výsledkem bude kontrola vymezení vůle podle vztahu ![]() .
.
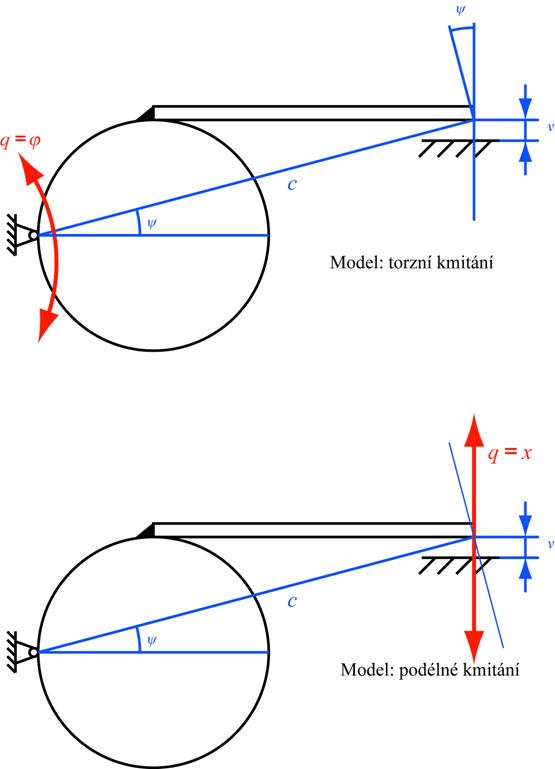
Mezi oběma přístupy, na základě kterých musí být dosaženy stejné výsledky a stejné závěry platí vztahy
![]()
V obou případech je nutno
stanovit úhel ![]() , pro která platí
, pro která platí
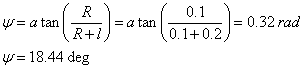
a také vzdálenost ![]() , pro kterou
platí
, pro kterou
platí
![]()
Poznámky
· Při řešení nebudou uvažovány tíhové síly, protože soustava je v rovnovážné poloze.
· Pro odlišení zobecněných veličin (hmotnosti, tuhosti, tlumení a vnější síly), které jsou označeny v teoretické části od označení, které je použito v příkladu, budou zde tyto veličiny označeny nahoře hvězdičkou.
Řešení dle 1. přístupu ![]()
Pro aplikaci Lagrangeových rovnic druhého druhu je nutno stanovit kinetickou a potenciální energii, tlumící funkci a práci (výkon) vnějších sil, které nemají potenciál.
Kinetická energie
![]()
Zobecněná hmotnost má charakter osového momentu setrvačnosti k ose kolmé na rovinu kmitání. Při jejím stanovení je nutno použít Steinerovu větu.
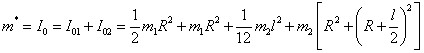
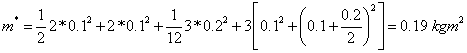
Potenciální energie
Při stanovení potenciální energie je nutno vzít v úvahu jednak pohyb středu kotouče, kde je vázána pružina a potom pohyb základu, na který je pružina vázána.
![]()
Derivace potenciální energie podle zobecněné souřadnice
![]()
odkud pro zobecněnou tuhost je
![]()
Pro zatlumenou energii platí
![]()
odkud pro zobecněné tlumení je
![]()
Amplituda budících sil, které nemají potenciál bude stanovena na základě derivace potenciální energie podle zobecněné souřadnice
![]()
S ohledem na tvar kinetické energie, její parciální derivace podle zobecněné souřadnice je nulová. Výsledný tvar pohybové rovnice pak je
![]()
Vlastní frekvence volného netlumeného kmitání
![]()
Součinitel doznívání
![]()
Vlastní frekvence tlumeného kmitání
![]()
Na obr. 10 je nakreslena amplitudová charakteristika pro daný příklad.
Poměrný útlum následně je
![]()
S ohledem na rozsah
provozního buzení ![]() a vlastní
frekvenci tlumeného
kmitání
a vlastní
frekvenci tlumeného
kmitání ![]() , nastane v pásmu provozního
buzení rezonanční stav,
při kterém bude maximální odezva. Stačí tedy zkontrolovat amplitudu při
rezonančním stavu. Obecný vztah pro odezvu je
, nastane v pásmu provozního
buzení rezonanční stav,
při kterém bude maximální odezva. Stačí tedy zkontrolovat amplitudu při
rezonančním stavu. Obecný vztah pro odezvu je
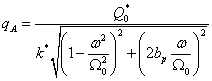
Rezonanční
stav nastane, kdy je ![]() , což po dosazení
, což po dosazení
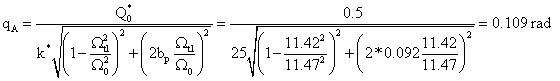
Svislé posunutí koncového bodu na tyčce je dáno vztahem
![]()
Vzhledem k tomu, že
svislá amplituda kmitání koncového bodu je větší
než vůle ![]() ,
nastane v daném pásmu provozního buzení
vymezení vůle.
,
nastane v daném pásmu provozního buzení
vymezení vůle.
Poznámka: Obdobně by se postupovalo v případě, že by se pohybovalo základní těleso, na které je vázán tlumící člen. budící účinky by byly stanovena ze vztahu pro derivaci zatlumené funkce.
13.2 Příklad 2 – buzení rotujícím tělesem
Je dána
soustava těles podle obrázku. Kotouč o
hmotnosti ![]() a poloměru
a poloměru ![]() je pevně spojen s tyčí o
hmotnosti
je pevně spojen s tyčí o
hmotnosti ![]() délky
délky ![]() .
. ![]() ,
, ![]() ,
, ![]() ,
, ![]() , nevývaha
, nevývaha ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
Soustava se nachází ve staticky rovnovážné poloze a
předpokládejte malé kmity kolem této polohy. Předpokládejte, že dynamický
systém je lineární.
.
Soustava se nachází ve staticky rovnovážné poloze a
předpokládejte malé kmity kolem této polohy. Předpokládejte, že dynamický
systém je lineární.
Pro danou soustavu řešte:
3. Stanovte vlastní frekvenci netlumeného a tlumeného kmitání a znázorněte amplitudovou charakteristiku.
4. Rozhodněte, zda v pásmu provozního buzení nastane vymezení vůle v.
Rozbor úlohy
Soustava těles představuje soustavu, která má jeden stupeň volnosti. K sestavení pohybové rovnice budou využity Lagrangeovy rovnice druhého druhu. K analýze kmitání lze přistupovat dvěma způsoby.
Schéma prvního
způsobu je uvedena výše. Jako zobecněná
souřadnice je zvoleno natočení soustavy, tedy ![]() . Výsledkem bude kontrola
vymezení vůle podle vztahu
. Výsledkem bude kontrola
vymezení vůle podle vztahu ![]() .
.
Schéma druhého
způsobu je uvedena výše. Jako zobecněná
souřadnice je zvoleno posunutí koncového bodu na
tyčce, tedy ![]() .
Výsledkem bude kontrola vymezení vůle podle vztahu
.
Výsledkem bude kontrola vymezení vůle podle vztahu ![]() .
.
Mezi oběma přístupy, na základě kterých musí být dosaženy stejné výsledky a stejné závěry platí vztahy
![]()
V obou případech je nutno
stanovit úhel ![]() , pro která platí
, pro která platí
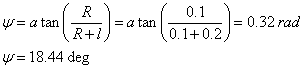
a také vzdálenost ![]() , pro kterou
platí
, pro kterou
platí
![]()
Poznámky
· Při řešení nebudou uvažovány tíhové síly, protože soustava je v rovnovážné poloze.
· Pro odlišení zobecněných veličin (hmotnosti, tuhosti, tlumení a vnější síly), které jsou označeny v teoretické části od označení, které je použito v příkladu, budou zde tyto veličiny označeny nahoře hvězdičkou.
Řešení dle 1. přístupu ![]()
Pro aplikaci Lagrangeových rovnic druhého druhu je nutno stanovit kinetickou a potenciální energii, tlumící funkci a práci (výkon) vnějších sil, které nemají potenciál.
Kinetická energie
![]()
Zobecněná hmotnost má charakter osového momentu setrvačnosti k ose kolmé na rovinu kmitání. Při jejím stanovení je nutno použít Steinerovu větu.
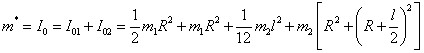
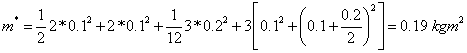
Potenciální energie
Při stanovení potenciální energie je nutno vzít v úvahu jednak pohyb středu kotouče, kde je vázána pružina a potom pohyb základu, na který je pružina vázána.
![]()
odkud pro zobecněnou tuhost je
![]()
Pro zatlumenou energii platí
![]()
odkud pro zobecněné tlumení je
![]()
Buzení bude stanoveno na základě buzení rotujícím tělesem
![]()
S ohledem na tvar kinetické energie, její parciální derivace podle zobecněné souřadnice je nulová. Výsledný tvar pohybové rovnice pak je
![]()
Vlastní frekvence volného netlumeného kmitání
![]()
Součinitel doznívání
![]()
Vlastní frekvence tlumeného kmitání
![]()
Na obr. 10 je nakreslena amplitudová charakteristika. Poměrný útlum následně je
![]()
S ohledem na rozsah
provozního buzení ![]() a vlastní
frekvenci tlumeného
kmitání
a vlastní
frekvenci tlumeného
kmitání ![]() , nastane v pásmu provozního
buzení rezonanční stav,
při kterém bude maximální odezva. Stačí tedy zkontrolovat amplitudu při
rezonančním stavu. Obecný vztah pro odezvu je
, nastane v pásmu provozního
buzení rezonanční stav,
při kterém bude maximální odezva. Stačí tedy zkontrolovat amplitudu při
rezonančním stavu. Obecný vztah pro odezvu je
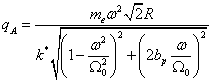
Rezonanční
stav nastane, kdy je ![]() , což po dosazení
, což po dosazení
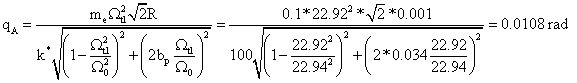
Svislé posunutí koncového bodu na tyčce je dáno vztahem
![]()
Vzhledem k tomu, že
svislá amplituda kmitání
koncového bodu je menší než vůle ![]() , nenastane v daném pásmu provozního
buzení vymezení vůle.
, nenastane v daném pásmu provozního
buzení vymezení vůle.